Ответ 1
Он назвал Парадокс дня рождения.
Согласно этой формуле из Википедии:
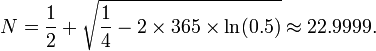
но вместо 365 10! вам потребуется всего около 2200 примеров, чтобы иметь 50% вероятность столкновения, и вы находитесь выше этого.
Для списка из 10 ints есть 10! возможных порядков или перестановок. Почему random.shuffle дает дубликаты после 5000 попыток?
>>> L = range(10)
>>> rL = list()
>>> for i in range(5000):
... random.shuffle(L)
... rL.append(L[:])
...
>>> rL = [tuple(e) for e in rL]
>>> len(set(rL))
4997
>>> for i,t in enumerate(rL):
... if rL.count(t) > 1:
... print i,t
...
102 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
258 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
892 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
2878 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
4123 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
4633 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
>>> 10*9*8*7*6*5*4*3*2
3628800
>>> 2**19937 - 1
431542479738816264805523551633791983905393 [snip]
>>> L = list()
>>> for i in range(5000):
... L.append(random.choice(xrange(3628800)))
...
>>> len(set(L))
4997
Изменить: FWIW, если вероятность того, что две одинаковые для одной пары не равны: p = (10! - 1)/10! и количество комбинаций: C = 5000!/4998! * 2!= 5000 * 4999/2 то вероятность наличия дубликата:
>>> import math
>>> f = math.factorial(10)
>>> p = 1.0*(f-1)/f
>>> C = 5000.0*4999/2
>>> 1 - p**C
0.96806256495611798
Он назвал Парадокс дня рождения.
Согласно этой формуле из Википедии:
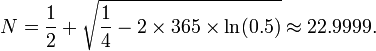
но вместо 365 10! вам потребуется всего около 2200 примеров, чтобы иметь 50% вероятность столкновения, и вы находитесь выше этого.
Потому что это... случайный! Если вы хотите, чтобы все перестановки просто использовали itertools.permutations.
может быть, потому что это RANDOM? Случайное не означает, что это не повторение, это означает, что это СЛУЧАЙНО, что означает, что теоретически он может возвращать тот же самый ответ каждый раз, но не возможно, но возможно.