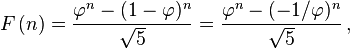Проверьте, является ли число фибоначчи
Я знаю, как составить список номеров Fibonacci, но я не знаю, как я могу проверить, принадлежит ли данный номер списку фибоначчи - один из способов, который приходит в голову, - это создать список фидов. номера до этого числа и посмотреть, принадлежит ли он массиву, но должен быть другой, более простой и быстрый метод.
Любые идеи?
Ответы
Ответ 1
Очень хороший тест состоит в том, что N является числом Фибоначчи тогда и только тогда, когда 5 N^2 + 4 или 5N^2 – 4 - это квадратное число. Для идей о том, как эффективно проверить, что число является квадратным, обратитесь к SO обсуждение.
Надеюсь, что это поможет
Ответ 2
Положительное целое число ω является числом Фибоначчи тогда и только тогда, когда один из 5ω 2 + 4 и 5ω 2 - 4 - идеальный квадрат.
Подробнее см. Номера Faboulous Fibonacci.
![alt text]()
Ответ 3
В то время как несколько человек указывают на идеальное квадратное решение, оно включает в себя возведение в квадрат числа Фибоначчи, часто приводящее к массивному продукту.
Существует менее 80 чисел Фибоначчи, которые могут быть даже сохранены в стандартном 64-битном целочисленном значении.
Вот мое решение, которое работает полностью меньше, чем число, которое нужно проверить.
(написанный на С#, используя базовые типы, такие как double и long. Но алгоритм должен работать отлично для больших типов.)
static bool IsFib(long T, out long idx)
{
double root5 = Math.Sqrt(5);
double phi = (1 + root5) / 2;
idx = (long)Math.Floor( Math.Log(T*root5) / Math.Log(phi) + 0.5 );
long u = (long)Math.Floor( Math.Pow(phi, idx)/root5 + 0.5);
return (u == T);
}
Спустя более 4 лет после того, как я написал этот ответ, комментатор спросил о втором параметре, переданном out.
Параметр №2 - это "Индекс" в последовательность Фибоначчи.
Если тестируемое значение T является числом Фибоначчи, то idx будет индексом 1 этого числа в последовательности Фибоначчи. (за одним заметным исключением)
Последовательность Фибоначчи 1 1 2 3 5 8 13 и т.д.
3 - четвертое число в последовательности: IsFib(3, out idx); вернет true и значение 4.
8 - 6-е число в последовательности: IsFib(8, out idx); вернет true и значение 6.
13 - 7-е число; IsFib(13, out idx); вернет true и значение 7.
Единственное исключение - IsFib(1, out idx);, которое вернет 2, хотя значение 1 появляется как в индексе 1, так и в 2.
Если IsFib передается число без Фибоначчи, оно вернет false, а значение idx будет индексом наибольшего числа Фибоначчи меньше T.
16 не является значением Фибоначчи.
IsFib(16, out idx); вернет false и значение 7.
Вы можете использовать Binet Formula для преобразования индекса 7 в значение Фибоначчи 13, которое является наибольшим числом менее 16.
Ответ 4
#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
echo "$victim is a fibonacci number"
else
echo "$victim aint"
fi
Ответ 5
Если ваши номера имеют ограниченный размер, чем просто положить все числа фибоначчи ниже верхней границы в хеш-таблицу, а тестовая сдерживающая способность сделает трюк. Число фибоначчи очень мало (например, только 38 ниже 5 млн.), Так как они растут экспоненциально.
Если ваши номера не имеют ограниченного размера, то предлагаемый трюк с квадратным тестированием почти наверняка будет медленнее, чем генерация последовательности фибоначчи, пока номер не будет найден или превышен.
Ответ 6
Положительное целое число ω - число Фибоначчи
В том и только в том случае, если один из 5ω 2 + 4 и 5ω 2- 4 - идеальный квадрат
из (Fabulous) номеров FIBONACCI Альфреда Посаменье и Ингмара Леманна
bool isFibonacci(int w)
{
double X1 = 5 * Math.Pow(w, 2) + 4;
double X2 = 5 * Math.Pow(w, 2) - 4;
long X1_sqrt = (long)Math.Sqrt(X1);
long X2_sqrt = (long)Math.Sqrt(X2);
return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}
Я скопировал его из этого источника
Фрагмент, который печатает числа Фибоначчи между 1k и 10k.
for (int i = 1000; i < 10000; i++)
{
if (isFibonacci(i))
Console.Write(" "+i);
}
OMG Есть только ЧЕТЫРЕ!!!
С другим методом
from math import *
phi = 1.61803399
sqrt5 = sqrt(5)
def F(n):
return int((phi**n - (1-phi)**n) /sqrt5)
def isFibonacci(z):
return F(int(floor(log(sqrt5*z,phi)+0.5))) == z
print [i for i in range(1000,10000) if isFibonacci(i)]
Ответ 7
На пути к решению взгляните на Формулу Бине.
(Ищите "выражение закрытой формы" под номер Фибоначчи в Википедии)
В нем говорится, что последовательность числа Фибоначчи создается простой замкнутой формулой:
![alt text]()
Я верю, что если вы решите для n и проверьте, является ли n целое число, вы получите ответ.
Изменить. Как указывает @psmears, в той же статье в Википедии есть раздел об обнаружении чисел Фибоначчи. Википедия - отличный источник.
Ответ 8
См. раздел "Признание чисел Фибоначчи" в статье статьи о Фибоначчи.
Ответ 9
Так как числа Фибоначчи растут экспоненциально, метод, который вы предлагаете, довольно быстро.
Другим является this.
Ответ 10
Из Википедии: http://en.wikipedia.org/wiki/Fibonacci_number
Положительное целое число z является фибоначчи число тогда и только тогда, когда один из 5z ^ 2 + 4 или 5z ^ 2 - 4 - идеальный квадрат.
Ответ 11
Основываясь на более ранних ответах меня и psmears, я написал этот код С#.
Он медленно проходит шаги, и его можно явно уменьшить и оптимизировать:
// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
// eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
double root5 = Math.Sqrt(5);
double PSI = (1 + root5) / 2;
// For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number
double a;
a = T*root5;
a = Math.Log(a) / Math.Log(PSI);
a += 0.5;
a = Math.Floor(a);
idx = (Int32)a;
long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);
if (u == T)
{
return true;
}
else
{
idx = 0;
return false;
}
}
Тестирование показывает эти работы для первых 69 чисел Фибоначчи, но разбивается на 70-е.
F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails
В целом, если вы не используете какую-либо библиотеку BigInt, вероятно, лучше иметь простую таблицу поиска чисел Фибоначчи и проверить, а не запускать алгоритм.
Список первых 300 номеров легко доступен онлайн.
Но в этом коде описывается работоспособный алгоритм, если вы обладаете достаточной точностью и не переполняете свою систему представления чисел.
Ответ 12
Общее выражение для числа Фибоначчи является
F (n) = [[(1 + sqrt (5))/2] sup n + 1 - [(1-sqrt (5))/2] sup n + 1]/sqrt (5)..... (*)
Вторая экспонента стремится к нулю при больших n и выполняя
числовых операций получаем F (n) = [(1.618) sup n + 1]/2.236
Если K - число, подлежащее проверке, log (k * 2.2336)/log (1.618) должно быть целым числом!
Пример для K, равный 13, мой калькулятор дает ответ 7.00246
Для K равным 14 ответ равен 7.1564.
Вы можете увеличить доверие к результату, взяв самое близкое целое к
ответьте и замените в (*), чтобы подтвердить, что результатом является K
Ответ 13
Re: Ahmad code - более простой подход без рекурсии или указателей, довольно наивный, но для чего-то не хватает вычислительной мощности для чего-либо, кроме действительно титанических чисел (примерно 2N дополнений для проверки номера N-го фибра, который на современной машине в худшем случае займет миллисекунды)
//возвращает pos, если он находит что-либо, 0, если это не так (C/С++ рассматривает любое значение!= 0 как true, поэтому тот же конечный результат)
int isFib (long n)
{
int pos = 2;
long last = 1;
long current = 1;
long temp;
while (current < n)
{
temp = last;
last = current;
current = current + temp;
pos++;
}
if (current == n)
return pos;
else
return 0;
}
Ответ 14
Насколько велики числа, с которыми вы имеете дело?
Может ли таблица поиска работать для вас? (предварительно вычисленный список номеров, которые вы можете найти)
Там также выражение закрытой формы, которое, я думаю, вы можете инвертировать, чтобы аналитически получить ответ (хотя я не математик, поэтому я не могу обещать, что это предложение имеет смысл)
Ответ 15
Я провел несколько тестов по представленным здесь методам вместе с простым добавлением, предварительным вычислением массива и воспоминанием результатов в хеше. Для Perl, по крайней мере, метод квадратизации немного быстрее, чем логарифмический метод, возможно, на 20% быстрее. Как указывает Абеленкий, это компромисс между тем, есть ли у вас место для квадратизации номеров бит.
Конечно, самым быстрым способом является хэш всех чисел Фибоначчи в вашем доменном пространстве. Вдоль линий другой точки, которую производит абеленки, есть только 94 из этих присосок, которые меньше 2 ^ 64.
Вы должны просто предварительно вычислить их и поместить их в хеш-Perl, словарь Python или что-то еще.
Свойства чисел Фибоначчи очень интересны, но использование их для определения того, является ли какое-то целое число в компьютерной программе единым, подобно написанию подпрограммы для вычисления pi при каждом запуске программы.
Ответ 16
Это мое решение. Я не уверен, что это тесты. Надеюсь, это поможет!
def is_fibonacci?(i)
a,b=0,1
until b >= i
a,b=b,a+b
return true if b == i
end
end
что a, b = b, a + b делает
0, 1 = 1, 0 +1
1, 1 = 1, 1 + 1
1, 2 = 2, 1 + 2
2, 3 = 3, 2 + 3
fib1 = fib2
fib2 = fib1 + fib2
Ответ 17
A Scala версия -
def isFib(n: Int): Boolean = {
def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {
if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)
}
checkFib()
}
Ответ 18
Java-решение может быть выполнено, как показано ниже. Но все же его можно оптимизировать
Следующее решение работает для
T - нет тестовых случаев,
N - диапазон числа
import java.util.Scanner;
import java.math.BigDecimal;
import java.math.RoundingMode;
public class FibonacciTester {
private static BigDecimal zero = BigDecimal.valueOf(0);
private static BigDecimal one = BigDecimal.valueOf(1);
private static BigDecimal two = BigDecimal.valueOf(2);
private static BigDecimal four = BigDecimal.valueOf(4);
private static BigDecimal five = BigDecimal.valueOf(5);
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
BigDecimal[] inputs = new BigDecimal[n];
for (int i = 0; i < n; i++) {
inputs[i] = sc.nextBigDecimal();
}
for (int i = 0; i < inputs.length; i++) {
if (isFibonacci(inputs[i]))
System.out.println("IsFibo");
else
System.out.println("IsNotFibo");
}
}
public static boolean isFibonacci(BigDecimal num) {
if (num.compareTo(zero) <= 0) {
return false;
}
BigDecimal base = num.multiply(num).multiply(five);
BigDecimal possibility1 = base.add(four);
BigDecimal possibility2 = base.subtract(four);
return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
}
public static boolean isPerfectSquare(BigDecimal num) {
BigDecimal squareRoot = one;
BigDecimal square = one;
BigDecimal i = one;
BigDecimal newSquareRoot;
int comparison = -1;
while (comparison != 0) {
if (comparison < 0) {
i = i.multiply(two);
newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
} else {
i = i.divide(two);
newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
}
if (newSquareRoot.compareTo(squareRoot) == 0) {
return false;
}
squareRoot = newSquareRoot;
square = squareRoot.multiply(squareRoot);
comparison = square.compareTo(num);
}
return true;
}
}
Ответ 19
int isfib(int n /* number */, int &pos /* position */)
{
if (n == 1)
{
pos=2; // 1 1
return 1;
}
else if (n == 2)
{
pos=3; // 1 1 2
return 1;
}
else
{
int m = n /2;
int p, q, x, y;
int t1=0, t2 =0;
for (int i = m; i < n; i++)
{
p = i;
q = n -p; // p + q = n
t1 = isfib(p, x);
if (t1) t2 = isfib(q, y);
if (t1 && t2 && x == y +1)
{
pos = x+1;
return 1; //true
}
}
pos = -1;
return 0; //false
}
}
Как насчет этого?
Ответ 20
#include <stdio.h>
#include <math.h>
int main()
{
int number_entered, x, y;
printf("Please enter a number.\n");
scanf("%d", &number_entered);
x = y = 5 * number_entered^2 + 4; /*Test if 5N^2 + 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
printf("That number is in the Fibonacci sequence.\n");
}
x = y = 5 * number_entered^2 - 4; /*Test if 5N^2 - 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
printf("That number is in the Fibonacci sequence.\n");
}
else
{
printf("That number isn't in the Fibonacci sequence.\n");
}
return 0;
}
Будет ли это работать?