Почему pyplot.contour() требует, чтобы Z был 2D-массивом?
Функция matplotlib.pyplot.contour() принимает 3 входных массива X, Y и Z.
Массивы X и Y определяют x- и y-координаты точек, а Z задает соответствующее значение интересующей функции, оцениваемой в точках.
Я понимаю, что np.meshgrid() позволяет легко создавать массивы, которые служат аргументами для contour():
X = np.arange(0,5,0.01)
Y = np.arange(0,3,0.01)
X_grid, Y_grid = np.meshgrid(X,Y)
Z_grid = X_grid**2 + Y_grid**2
plt.contour(X_grid, Y_grid, Z_grid) # Works fine
Это прекрасно работает. И удобно, это отлично работает:
plt.contour(X, Y, Z_grid) # Works fine too
Однако почему вход Z требуется как 2D-массив?
Почему что-то вроде следующего недопустимо, хотя он указывает все одинаковые данные, соответствующие соответствующим образом?
plt.contour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel()) # Disallowed
Кроме того, что такое семантика, когда указан только Z (без соответствующих X и Y)?
Ответы
Ответ 1
Глядя на документацию по contour можно обнаружить, что существует несколько способов вызова этой функции, например, contour(Z) или contour(X,Y,Z). Таким образом, вы обнаружите, что для этого вообще не требуется никаких значений X или Y
Однако, чтобы построить контур, базовая сетка должна быть известна функции. contour Matplotlib основан на прямоугольной сетке. Но даже в этом случае разрешение contour(z), где z является одномерным массивом, лишает возможности узнать, как должно быть построено поле. В случае contour(Z) где Z является двумерным массивом, его форма однозначно задает сетку для графика.
Как только эта сетка известна, становится неважно, сглажены ли необязательные массивы X и Y; что фактически говорит нам документация:
X и Y оба должны быть двумерными и иметь ту же форму, что и Z, или они оба должны быть одномерными, так что len (X) - это число столбцов в Z, а len (Y) - это количество строк в Z.
Также совершенно очевидно, что некоторые функции, такие как plt.contour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel()) не могут создать контурный график, потому что вся информация о форме сетки теряется и отсутствует Таким образом, функция контура может знать, как интерпретировать данные. Например, если len(Z_grid.ravel()) == 12, основная форма сетки может быть любой из (1,12), (2,6), (3,4), (4,3), (6,2), (12,1).
Конечно, возможный выход может заключаться в том, чтобы разрешить одномерные массивы и ввести shape аргумента, например, plt.contour(x,y,z, shape=(6,2)). Это, однако, не так, поэтому вы должны учитывать тот факт, что Z должен быть 2D.
Тем не менее, если вы ищете способ получения графического графика со сплюснутыми (выровненными) массивами, это возможно с помощью plt.tricontour().
plt.tricontour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel())
Здесь треугольная сетка будет производиться внутри с использованием триангуляции Делоне. Поэтому даже полностью рандомизированные точки дают хороший результат, как видно на следующем рисунке, где это сравнивается с теми же случайными точками, заданными для contour.
![enter image description here]()
(Вот код для создания этой картины)
Ответ 2
Фактический код алгоритма позади plt.contour можно найти в _ countour.cpp. Это довольно сложный C-код, поэтому его трудно точно следовать, но если бы я пытался создать код, генерирующий контуры, я бы сделал это следующим образом. Выберите точку (x, y) на границе и исправьте ее значение z. Итерируйте по соседним точкам и выберите тот, для которого z-значение является самым близким к z-значению первой точки. Продолжайте итерацию для новой точки, выберите ближайшую точку с близким к z значением z (но убедитесь, что вы не вернетесь к точке, которую вы только что посетили, поэтому вам нужно идти в каком-то "направлении" ), и продолжайте, пока не получите цикл или достичь некоторой границы.
Кажется, что в _counter.cpp реализовано что-то близкое (но немного более сложное).
Как видно из неофициального описания алгоритма, вы должны найти точку, которая находится "рядом" с текущей. Это легко сделать, если у вас прямоугольная сетка точек (требуется примерно 4 или 8 итераций: (x[i+1][j], y[i+1][j]), (x[i][j+1], y[i][j+1]), (x[i-1][j], y[i-1][j]) и т.д.). Но если у вас есть случайно выбранные точки (без какого-либо определенного порядка), эта проблема становится сложной: вам нужно перебирать все точки, которые вы должны найти рядом, и сделать следующий шаг. сложность такого шага O(n), где n - количество точек (обычно это квадрат размера изображения). Таким образом, алгоритм становится намного медленнее, если у вас нет прямоугольной сетки.
Вот почему вам действительно нужны три 2d-массива, которые соответствуют x, y и z некоторых точек, расположенных над некоторой прямоугольной сеткой.
Как вы правильно отметили, x и y могут быть 1d-массивами. В этом случае соответствующие 2d-массивы реконструируются с помощью meshgrid. Однако в этом случае вы должны иметь z как 2d-массив.
Если указан только z, x и y являются range соответствующих длин.
ИЗМЕНИТЬ. Вы можете попытаться "подделать" двумерные массивы x, y и z таким образом, чтобы x и y не формировали прямоугольную сетку, чтобы проверить правильность моих допущений.
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
x = np.random.uniform(-3, 3, size=10000)
y = np.random.uniform(-3, 3, size=10000)
z = x**2 + y**2
X, Y, Z = (u.reshape(100, 100) for u in (x, y, z))
plt.contour(X, Y, Z)
![Неверный результат]()
Как вы видите, изображение не похоже на что-либо близкое к правильному графу, если (x, y, z) являются лишь некоторыми случайными точками.
Теперь предположим, что x сортируется как шаг предварительной обработки, как предлагает @dhrummel в комментариях. Обратите внимание, что мы не можем сортировать x и y одновременно, поскольку они не являются независимыми (мы хотим сохранить одни и те же точки).
x = np.random.uniform(-3, 3, size=10000)
y = np.random.uniform(-3, 3, size=10000)
z = x**2 + y**2
xyz = np.array([x, y, z]).T
x, y, z = xyz[xyz[:, 0].argsort()].T
assert (x == np.sort(x)).all()
X, Y, Z = (u.reshape(100, 100) for u in (x, y, z))
plt.contour(X, Y, Z)
![x отсортировано сейчас]()
Опять же, изображение неверно из-за того, что y не сортируются (в каждом столбце), как они были, если бы мы имели прямоугольную сетку вместо некоторых случайных точек.
Ответ 3
Причиной X и Y для 2D является следующее.
Z соответствует каждой координате (x, y) в системе осей соответствующей "глубины" для создания 3D-графика с координатами x, y и z.
Теперь предположим, что мы хотим указать на произвольную точку в системе осей.
Мы можем это сделать, предоставив для этой точки координаты x и y (x, y). Например (0,0).
Теперь рассмотрим "строку" со значением x 1. На этой строке есть ряд значений n y, которые выглядят как-то вроде:
![введите описание изображения здесь]()
Если мы построим эти строки для всех значений x и значений y, мы получим что-л. как:
![введите описание изображения здесь]()
Как вы можете видеть, у нас есть 2D-аннотация, состоящая из массивов 2 2D, одна для значений x, которая имеет форму:
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
#--> Two dimensional x values array
и один для значений y, которые имеют форму:
10 10 10 10 10 10 10 10 10 10
9 9 9 9 9 9 9 9 9 9
8 8 8 8 8 8 8 8 8 8
...
1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0
#--> Two dimensional y values array
Эти два вместе обеспечивают координаты (x, y) для каждой точки в системе координат. Теперь мы можем построить для каждой точки "глубина" значение Z (координата z).
Теперь также очевидно, почему переменная Z должна быть двумерной с формой (len (x), len (y)), поскольку в противном случае она не может обеспечить значение для всех точек.
Такое поведение может быть реализовано либо путем предоставления массивов 2D x, y и z функции OR: предоставить функции 1D x и y функции, а функция внутренне создает 2D-сетку из значений x и y с помощью smth. как X, Y = np.meshgrid(x, y), но тем не менее z должно быть двумерным.
Ответ 4
Позвольте мне объяснить это простым способом, так как я думал, что Z не должен быть также 2D. contourf() нужны X и Y, чтобы построить свое собственное пространство, и отношение Z (X, Y), чтобы построить полное пространство, а не просто использовать несколько точек с 1D X, Y, Z информацией.
Ответ 5
Представьте, что вы хотите построить трехмерный график. У вас есть набор из x точек и набор из y точек. Цель состоит в том, чтобы получить значение z для каждой пары x и y, или, другими словами, вам нужна функция f, которая генерирует значение z так что z = f(x, y).
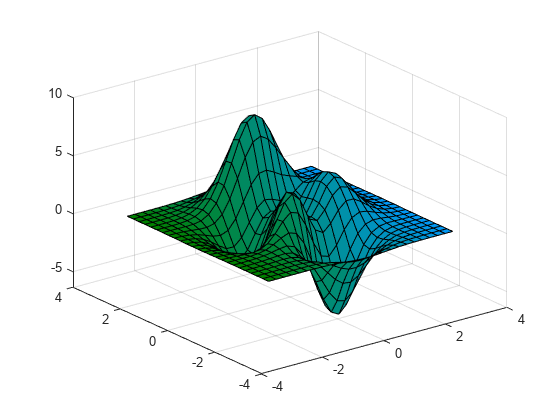
Вот хороший пример (взят из MathWorks):
![surf]()
Координаты x и y находятся внизу справа и внизу слева соответственно. У вас будет функция f такая, что для каждой пары x и y мы генерируем значение z. Поэтому в предоставленном numpy.meshgrid вызов numpy.meshgrid сгенерирует два двумерных массива, так что для каждого уникального пространственного местоположения мы будем наблюдать значения x и y которые являются уникальными для этого местоположения.
Например, давайте использовать очень маленький пример:
In [1]: import numpy as np
In [2]: x, y = np.meshgrid(np.linspace(-1, 1, 3), np.linspace(-1, 1, 3))
In [3]: x
Out[3]:
array([[-1., 0., 1.],
[-1., 0., 1.],
[-1., 0., 1.]])
In [4]: y
Out[4]:
array([[-1., -1., -1.],
[ 0., 0., 0.],
[ 1., 1., 1.]])
Взгляните, например, на строку № 2 и колонку № 1 (я начинаю индексирование с 0 до 100). Это означает, что в этом пространственном местоположении мы будем иметь координаты x = 0. и y = 1. numpy.meshgrid дает нам пару x и y которая требуется для генерации значения z по этой конкретной координате. Для удобства он просто разделен на два 2D-массива.
Теперь, что, наконец, нужно поместить в вашу переменную z это то, что она должна использовать функцию f и обрабатывать то, что выводится для каждого значения в x и его соответствующего y.
В явном виде вам нужно будет сформулировать двумерный массив z, чтобы:
z = [f(-1, -1) f(0, -1) f(1, -1)]
[f(-1, 0) f(0, 0) f(1, 0)]
[f(-1, 1) f(0, 1) f(1, 1)]
Посмотрите очень внимательно на пространственное расположение слагаемых x и y. Мы генерируем 9 уникальных значений для каждой пары значений x и y. Значения x варьируются от -1 до 1 и одинаковы для y. Как только вы сгенерируете этот 2D-массив для z, вы можете использовать contourf для рисования наборов уровней, так что каждая линия контура даст вам набор всех возможных значений x и y которые равны одному и тому же значению z. Кроме того, между каждой соседней парой отдельных линий мы заполняем область между ними одним и тем же цветом.
Позвольте закончить это фактическим примером. Предположим, у нас есть функция f(x, y) = exp(-(x**2 + y**2)/10). Это двумерный гауссов со стандартным отклонением sqrt(5).
Поэтому, давайте создадим сетку из значений x и y, используйте это, чтобы сгенерировать значения z и нарисовать contourf график:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 101)
y = x
x, y = np.meshgrid(x, y)
z = np.exp(-(x**2 + y**2) / 10)
fig,ax2 = plt.subplots(1)
ax2.contourf(x,y,z)
plt.show()
Мы получаем:
![Contour]()