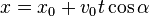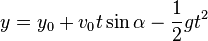Проблема баллистической кривой
Хорошо, я знаю, что это довольно не по теме для программистов, но все же мне это нужно для приложения, поэтому вот оно:
Баллистическая кривая (без ветра или любых других условий) определяется этими двумя строками:
![x coordinate]()
![y coordinate]()
Итак, есть проблема, что у вас есть 3 неизвестных значения: x, y и время t, но только 2 уравнения.
Вы не можете действительно вычислить все 3 только с этими значениями, я получил:
- скорость v
- угол Alpha
- исходные координаты
Таким образом, вы должны решить, какой из них указать.
Теперь у вас есть игра с двумя танками или что-то в этом роде, вы знаете, что у вас есть танк, и вы используете баллистику, вам нужно стрелять противником с углом уставки и мощностью.
Мне нужно знать, когда пуля попала в землю, она может быть в эфире, когда она летает, или предварительно вычислена.
Появляется моя проблема. Какой способ использовать? Предварительно вычислите или проверьте, чтобы попасть на землю на каждом шаге.
Если я хотел бы предварительно вычислить, мне нужно было бы знать высоту местности, которая, по логике, должна была бы быть постоянной, поскольку я не знаю, в какой х координаты. Если бы я знал Х, это означало бы, что перед моей башней стоит стена. Таким образом, единственный способ добиться результата, когда я ударил по земле, - это проверять интервалы времени, чтобы попасть в землю. Это также хорошо, потому что у местности нет вершины, статичной! Но разве это не слишком большие накладные расходы, которые можно было бы сделать намного проще? Вы столкнулись с такой проблемой/решением?
Спасибо заранее, что рельеф местности может быть плоским, используя линии или NURBS, поэтому, пожалуйста, для общего решения, а не для конкретного, как высота, на которую вы стреляете, будет влиять.
Ответы
Ответ 1
Вы можете вычислить путь снаряда y(x), решая одно уравнение для t и подставляя его в другое. Вы получаете
![y = x tan(theta) - x^2g/2(v cos(theta))^2]()
Тогда поиск точки посадки - это вопрос вычисления пересечений между этой функцией и функцией, определяющей высоту ландшафта. Одним из перекрестков станет точка запуска, а другая - точка посадки. (Если ваш ландшафт очень крутой и холмистый, может быть более двух пересечений, и в этом случае вы берете первый с x больше, чем точка запуска.) Вы можете использовать любой из алгоритмы коренного поиска для фактического вычисления пересечения; проверьте документацию о любых математических или игровых физических библиотеках, которые вы должны увидеть, если они предоставляют метод для этого.
Ответ 2
Дэвид Заславский неплохо ответил на ваш вопрос о решении уравнения, но если ваша конечная цель - простое баллистическое симуляция, я предлагаю вам вместо этого использовать векторную декомпозицию.
Используя векторное разложение, вы можете получить x- и y-compenent векторы вашего снаряда. Затем вы можете применить ускорение к каждому компоненту для учета силы тяжести, ветра и т.д. Затем вы можете обновить положение снаряда (x, y) каждый интервал в зависимости от времени.
Например:
double Speed = 100.0; // Speed rather than velocity, as it is only the magnitude
double Angle = 30.0; // Initial angle of 30º
doulbe Position[2] = {0.0,0.0}; // Set the origin to (0,0)
double xvelocity = Speed * Cos(Angle);
double yvelocity = Speed * Sin(Angle);
Затем, если вы можете внедрить простую функцию Update следующим образом:
void Update(double Time)
{
yvelocity = -9.8 * Time; // Apply gravity
Position[0] *= (xvelocity * Time); // update x position
Position[1] *= (yvelocity * time); // update y position
CheckCollisions(); // check for collisions
}
Конечно, это базовый пример очень, но вы можете построить его здесь.
Ответ 3
К счастью, это довольно простая кинематика.
Эти уравнения являются параметрическими: для любого заданного времени t они дают вам координаты x и y за это время. Все, что вам нужно сделать, это подключить начальную скорость v и угол a.
Если вы работаете на ровной поверхности, время, когда ваш снаряд возвращается, - это просто 2sin (a) v/g, т.е. вертикальная составляющая вашей скорости, деленная на ускорение вниз из-за силы тяжести. 2 состоит в том, что для того, чтобы скорость опустилась до 0, требуется столько времени, что в то же время снова ускорится. Как только вы узнаете время, которое вы можете решить для x.
Если ваш ландшафт не плоский, у вас есть дополнительная забава. Что-то, что вы могли бы попробовать, это разработать время для удара по земле на той же высоте, а затем исправить лишнее вертикальное расстояние. Это также изменит ваше горизонтальное расстояние, которое может снова повлиять на вашу высоту... но две или три регулировки и ошибка будет слишком мала для людей, чтобы заметить:)
Ответ 4
Я не уверен, что вы идете по этому правильному пути. Главное уравнение, которое вы хотите, s = si + vi * dt +.5 * adtdt. Это простое уравнение одного измерения, но оно чисто чисто для векторов.
Эффективно, si - ваше начальное положение, а vi - ваша начальная скорость, а a - ускорение из-за силы тяжести.
Чтобы сделать эту работу, создайте вектор для идеальной скорости горизонтальной морды и проецируйте его на угол запуска. Это ваш vi. Si будет концом ствола. Отсюда он суммирует и масштабирует вектор.
Ответ 5
Непрерывные функции не работают хорошо для компьютеров, поскольку компьютеры неявно дискретны: число с плавающей запятой или дискретное число, таймер дискретный, игровая сетка дискретна (даже если она использует "удваивает" ).
Итак, просто дискретизируйте уравнение, как предложил Джастин Холдслоу. Имеют векторы скорости и ускорения в каждом направлении (в вашем случае X и Y, вы также можете добавить Z). Обновите все векторы и позицию объекта в пространстве при каждом тике.
Обратите внимание, что результат не будет "точным". Чем меньше ваши значения "дельта" (грубая сетка), тем ближе вы будете к "точной" кривой. Чтобы точно знать, насколько близко - если вам интересно, найдите книгу по численному анализу и прочитайте первые несколько глав. Для практических целей вы можете просто немного экспериментировать.