Как суммировать последовательность?
Как я могу суммировать следующую последовательность:
⌊n/1⌋ + ⌊n/2⌋ + ⌊n/3⌋ + ... + ⌊n/n⌋
Это просто O (n) решение на С++:
#include <iostream>
int main()
{
int n;
std::cin>>n;
unsigned long long res=0;
for (int i=1;i<=n;i++)
{
res+= n/i;
}
std::cout<<res<<std::endl;
return 0;
}
Вы знаете лучшее решение, чем это? Я имею в виду O (1) или O (log (n)). Спасибо за ваше время:) и решения
Изменить:
Спасибо за все ваши ответы. Если кто-то хочет решение O (sqrt (n)):
Python:
import math
def seq_sum(n):
sqrtn = int(math.sqrt(n))
return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2
n = int(input())
print(seq_sum(n))
С++:
#include <iostream>
#include <cmath>
int main()
{
int n;
std::cin>>n;
int sqrtn = (int)(std::sqrt(n));
long long res2 = 0;
for (int i=1;i<=sqrtn;i++)
{
res2 +=2*(n/i);
}
res2 -= sqrtn*sqrtn;
std::cout<<res2<<std::endl;
return 0;
}
Ответы
Ответ 1
Это суммирующая функция дивизора Дирихле D (x). Используя следующую формулу (источник)
![D(x)]()
где
![u]()
предоставляет следующий O(sqrt(n)) psuedo-код (который действительно является допустимым Python):
def seq_sum(n):
sqrtn = int(math.sqrt(n))
return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2
Примечания:
- Оператор
// в Python является целым числом, то есть усечением, делением.
-
math.sqrt() используется в качестве иллюстрации. Строго говоря, это должно использовать точный целочисленный алгоритм с квадратным корнем вместо математики с плавающей запятой.
Ответ 2
Взято из статьи Википедии о суммирующей функции Divisor,
![enter image description here]()
где ![enter image description here]() . Это должно обеспечить временное решение
. Это должно обеспечить временное решение ![enter image description here]() .
.
EDIT: проблема с квадратным корнем целых чисел также может быть решена в квадратном корне или даже логарифмическом времени - на всякий случай, что это не очевидно.
Ответ 3
Проект Polymath набросает алгоритм вычисления этой функции за время O (n ^ (1/3 + o (1))), см. раздел 2.1 на страницах 8-9 из:
http://arxiv.org/abs/1009.3956
Алгоритм включает разбиение области на достаточно тонкие интервалы и оценку значения на каждом из них, где интервалы выбираются достаточно тонкими, чтобы оценка была точной при округлении до ближайшего целого. Поэтому вы вычисляете до некоторого диапазона напрямую (они предлагают 100n ^ (1/3), но вы можете модифицировать это с некоторой осторожностью), а затем делать остальные в этих тонких срезах.
См. запись OEIS для получения дополнительной информации об этой последовательности.
Изменить: теперь я вижу, что Kerrek SB упоминает этот алгоритм в комментариях. Справедливости ради, однако, я добавил комментарий к OEIS 5 лет назад, поэтому я не чувствую себя плохо для публикации "его" ответа.:)
Следует также упомянуть, что алгоритм O (1) невозможен, так как ответ вокруг n log n и, следовательно, даже для его записи требуется время > log n.
Ответ 4
Пусть деление всего числа {1, 2, 3, ..., n} на 2 группы: меньше или равно sqrt(n) и больше, чем sqrt(n). Для первой группы мы можем вычислить сумму простой итерацией. Для второй группы мы можем использовать следующее наблюдение: если a > sqrt(n), чем n / a < sqrt(n). Поэтому мы можем перебирать значение [n / i] = d (от 1 до sqrt(n)) и вычислять число таких i, что [n / i] = d. Его можно найти в O(1) для фиксированного d, используя тот факт, что [n / i] = d означает i * d <= n and i * (d + 1) > n, что дает [n / (d + 1)] < i <= [n / d].
Первая и вторая группы обрабатываются в O(sqrt(n)), что дает общее время O(sqrt(n)).
Ответ 5
Для больших n используйте формулу:
![enter image description here]()
где ![enter image description here]()
(![enter image description here]() - трансцендентное число.)
- трансцендентное число.)
Дополнительную информацию см. в Euler-Mascheroni constant.




 .
.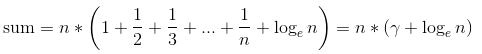
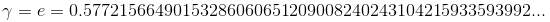
 - трансцендентное число.)
- трансцендентное число.)