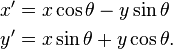Правильная тригонометрия для поворота точки вокруг начала

В любом из нижеприведенных подходов используется правильная математика для вращения точки? Если да, то какой из них правильный?

POINT rotate_point(float cx,float cy,float angle,POINT p)
{
  float s = sin(angle);
  float c = cos(angle);

  // translate point back to origin:
  p.x -= cx;
  p.y -= cy;

  // Which One Is Correct:
  // This?
  float xnew = p.x * c - p.y * s;
  float ynew = p.x * s + p.y * c;
  // Or This?
  float xnew = p.x * c + p.y * s;
  float ynew = -p.x * s + p.y * c;

  // translate point back:
  p.x = xnew + cx;
  p.y = ynew + cy;
}

Ответы

Ответ 1

Это зависит от того, как вы определяете angle. Если он измеряется против часовой стрелки (что является математическим соглашением), то правильное вращение будет вашим первым:

// This?
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;

Но если он измеряется по часовой стрелке, то второй правильный:

// Or This?
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;

Ответ 2

Из Википедии

Для выполнения вращения с использованием матриц поворачиваемая точка (x, y) записывается как вектор, а затем умножается на матрицу, вычисленную по углу θ, так:

где (x ', y') - координаты точки после вращения, а формулы для x 'и y' можно видеть как

Ответ 3

Это извлекается из моей собственной векторной библиотеки..

//----------------------------------------------------------------------------------
// Returns clockwise-rotated vector, using given angle and centered at vector
//----------------------------------------------------------------------------------
CVector2D   CVector2D::RotateVector(float fThetaRadian, const CVector2D& vector) const
{
    // Basically still similar operation with rotation on origin
    // except we treat given rotation center (vector) as our origin now
    float fNewX = this->X - vector.X;
    float fNewY = this->Y - vector.Y;

    CVector2D vectorRes(    cosf(fThetaRadian)* fNewX - sinf(fThetaRadian)* fNewY,
                            sinf(fThetaRadian)* fNewX + cosf(fThetaRadian)* fNewY);
    vectorRes += vector;
    return vectorRes;
}