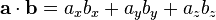Эффективное сравнение 100 000 векторов

Ответ 1

Во-первых, предварительно запрограммируйте свой векторный список, чтобы каждый вектор был нормализован. Обратите внимание, что теперь ваша функция сравнения T() теперь имеет величины, которые становятся постоянными, и формула может быть упрощена для нахождения наибольшего точечного произведения между вашим тестовым вектором и значениями в базе данных.

Теперь рассмотрим новую функцию D = расстояние между двумя точками в пространстве 60D. Это классический расстояние L2, используйте разницу между каждым компонентом, квадрат каждого, добавляйте все квадраты и берете квадратный корень из суммы. D (A, B) = sqrt ((A-B) ^ 2), где A и B представляют собой 60-мерные векторы.

Это можно расширить, однако, до D (A, B) = sqrt (A * A -2 * dot (A, B) + B * B). Тогда A и B являются величиной единицы измерения. И функция D монотонна, поэтому она не изменит порядок сортировки, если мы удалим sqrt() и посмотрим на квадратные расстояния. Это оставляет нам только -2 * точку (A, B). Таким образом, минимализующее расстояние в точности эквивалентно максимизации точечного произведения.

Таким образом, первоначальная метрика классификации T() может быть упрощена в поиске наивысшего точечного произведения между ноннализованными векторами. И это сравнение показано эквивалентно тому, что точка ближайшая указывает на точку образца в 60-D пространстве.

Итак, теперь все, что вам нужно сделать, это решить эквивалентную проблему "с учетом нормированной точки в пространстве 60D", перечислите 20 точек в базе данных нормализованных векторов образца, которые ближе всего к ней ".

Эта проблема хорошо понята... it K Ближайшие соседи. Существует множество алгоритмов для решения этого. Наиболее распространенным является классический деревья KD.

Но есть проблема. Деревья KD имеют поведение O (e ^ D). Высокая размерность быстро становится болезненной. И 60 измерений, безусловно, в этой чрезвычайно болезненной категории. Даже не пробуйте.

Однако существует несколько альтернативных общих методов для ближайшего соседа высокого D. Этот документ дает четкий метод.

Но на практике существует отличное решение, включающее еще одно преобразование. Если у вас есть метрическое пространство (которое вы делаете, или вы не будете использовать сравнение Tanimoto), вы можете уменьшить размерность проблемы с помощью 60-мерного вращения. Это звучит сложно и страшно, но это очень распространено. Это форма разложения по сингулярным значениям или разложение по собственным значениям. В статистике он известен как Анализ основных компонентов.

В основном это использует простой линейный расчет, чтобы найти, какие направления ваша база данных действительно охватывает. Вы можете свернуть 60 измерений до меньшего числа, возможно, как 3 или 4, и по-прежнему сможете точно определять ближайших соседей. Существует множество программных библиотек для этого на любом языке, например, здесь.

Наконец, вы сделаете классических ближайших соседей K, возможно, только в 3-10 измерениях. Вы можете поэкспериментировать для лучшего поведения. Там потрясающая библиотека для этого называется Ranger, но вы можете использовать и другие библиотеки. Большое преимущество - вам даже не нужно хранить все 60 компонентов ваших данных образца!

Вопрос о том, действительно ли ваши данные могут быть свернуты в сторону более низких измерений, не влияя на точность результатов. На практике разложение PCA может сообщить вам максимальную остаточную ошибку для любого выбранного вами предела D, поэтому вы можете быть уверены, что он работает. Поскольку точки сравнения основаны на метрике расстояния, они, скорее всего, сильно коррелированы, в отличие от значений хэш-таблицы.

Итак, вышесказанное:

• Нормализовать ваши векторы, превратив вашу проблему в проблему ближайшего соседа K в 60 измерениях
• Используйте анализ основных компонентов, чтобы уменьшить размерность до допустимого предела, например, 5 измерений.
• Используйте алгоритм K Nearest Neighbor, такой как библиотека дерева Ranger KD, чтобы найти близлежащие образцы.

Ответ 2

Update:

После того, как вы ясно дали понять, что 60 - это размер вашего пространства, а не длина векторов, ответ ниже не применим для вас, поэтому я сохраню его только для истории.

Так как ваши векторы нормированы, вы можете использовать kd-tree для поиска соседей внутри MBH инкрементного гиперволя.

Никакая база данных, о которой я знаю, имеет встроенную поддержку kd-tree, поэтому вы можете попробовать реализовать следующее решение в MySQL, если вы ищете ограниченное количество ближайших записей:

• Хранить проекции векторов на каждое возможное 2 -мерное пространство (принимает столбцы n * (n - 1) / 2)
• Индекс каждого из этих столбцов с индексом SPATIAL
• Выберите квадрат MBR данной области в пределах любой проекции. Произведение этих MBR даст вам гиперкуб ограниченного гиперволя, который будет содержать все векторы с расстоянием, не превышающим заданный.
• Найти все проекции во всех MBR с помощью MBRContains

Вам нужно будет отсортировать в пределах этого ограниченного диапазона значений.

Например, у вас есть набор 4 -мерных векторов с величиной 2:

(2, 0, 0, 0)
(1, 1, 1, 1)
(0, 2, 0, 0)
(-2, 0, 0, 0)

Вам необходимо сохранить их следующим образом:

p12  p13  p14  p23  p24  p34
---  ---  ---  ---  ---  ---
2,0  2,0  2,0  0,0  0,0  0,0
1,1  1,1  1,1  1,1  1,1  1,1
0,2  0,0  0,0  2,0  2,0  0,0
-2,0 -2,0 -2,0 0,0  0,0  0,0

Скажем, вы хотите подобие с первым вектором (2, 0, 0, 0) больше, чем 0.

Это означает наличие векторов внутри гиперкуба: (0, -2, -2, -2):(4, 2, 2, 2).

Вы задаете следующий запрос:

SELECT  *
FROM    vectors
WHERE   MBRContains('LineFromText(0 -2, 4 2)', p12)
        AND MBRContains('LineFromText(0 -2, 4 2)', p13)
        …

и т.д. для всех шести столбцов

Ответ 3

Таким образом, можно кэшировать следующую информацию:

• Норма выбранного вектора
• Точечный продукт A.B, повторно использующий его как для числителя, так и знаменателя при заданном вычислении T (A, B).

Если вам нужны только N ближайших векторов или если вы выполняете этот процесс сортировки несколько раз, могут быть доступны дополнительные трюки. (Наблюдения, такие как T (A, B) = T (B, A), кэширование векторных норм для всех векторов и, возможно, своего рода пороговая/пространственная сортировка).

Ответ 4

Чтобы сортировать что-то, вам нужен ключ сортировки для каждого элемента. Поэтому вам нужно будет обрабатывать каждую запись хотя бы один раз, чтобы вычислить ключ.

Это то, о чем вы думаете?

======= Перемещенный комментарий здесь:

Учитывая описание, вы не можете избежать просмотра всех записей, чтобы рассчитать коэффициент подобия. Если вы укажете базе данных, чтобы использовать коэффициент подобия в разделе "порядок", вы можете позволить ему выполнить всю тяжелую работу. Вы знакомы с SQL?

Ответ 5

Короче говоря, нет, возможно, нет способа избежать прохождения всех записей в базе данных. Один квалификатор на этом; если у вас есть значительное количество повторяющихся векторов, вы можете избежать повторной обработки точных повторов.

Ответ 6

Новый ответ

Сколько можно выполнить предварительную обработку? Можете ли вы заранее построить "окрестности" и указать, в каком окружении каждый вектор находится внутри базы данных? Это может позволить вам исключить из рассмотрения многие векторы.

Старый ответ ниже, который предположил, что 60 - величина всех векторов, а не размер.

Так как векторы имеют одинаковую длину (60), я думаю, что вы делаете слишком много математики. Разве вы не можете сделать точечный продукт выбранного по каждому кандидату?

В 3D:

Три умножения. В 2D это всего лишь два умножения.

Или это нарушает вашу идею сходства? Для меня наиболее похожими векторами являются те, у которых наименьшее расстояние angular между ними.

Ответ 7

Если вы готовы жить с приближениями, есть несколько способов избежать необходимости проходить через всю базу данных во время выполнения. В фоновом задании вы можете начать предварительное вычисление парных расстояний между векторами. Выполнение этого для всей базы данных - это огромное вычисление, но для этого не нужно быть готовым, чтобы оно было полезным (т.е. Начать вычислять расстояния до 100 случайных векторов для каждого вектора или т.д. Сохранять результаты в базе данных).

Тогда триангуляция. если расстояние d между вашим целевым вектором v и некоторым вектором v 'велико, то расстояние между v и всеми другими v' ', которые близки к v', будет большим (-ish) тоже, поэтому нет необходимости сравнивать (вам придется найти приемлемые определения "большого" ), хотя). Вы можете поэкспериментировать с повторением процесса для отброшенных векторов v '' и проверить, сколько выдержек времени выполнения вы можете избежать, прежде чем точность начнет уменьшаться. (сделайте тестовый набор "правильных" результатов для сравнений)

удачи.

ДСН

Ответ 8

Нет, нет?

Вам нужно всего лишь 99 999 против того, который вы выбрали (а не всех n(n-1)/2 возможных пар), конечно, но как можно ниже.

Глядя на ваш ответ на ответ nsanders, ясно, что вы уже на вершине этой части. Но я подумал о специальном случае, когда вычисление полного набора сравнений может быть победой. Если:

• список приходит медленно (скажем, вы получаете их из некоторой системы сбора данных с фиксированной низкой скоростью).
• Вы не знаете до конца, с кем хотите сравнить с
• У вас много хранения.
• вам нужно ответить быстро, когда вы выбираете один (и наивный подход не достаточно быстрый).
• Выглядит быстрее, чем вычисление

тогда вы можете предварительно вычислить данные по мере поступления данных и просто выполнить поиск по каждой паре во время сортировки. Это также может быть эффективным, если вы закончите делать много видов...

Ответ 9

Без ввода всех записей? Это кажется невозможным. Единственное, что вы можете сделать, это выполнить математику во время вставки (помня, что эквивалентность http://tex.nigma.be/T%2528A%252CB%2529%253DT%2528B%252CA%2529.png: P).

Это позволяет избежать запроса на проверку списка во всех остальных списках во время выполнения (но это может значительно увеличить пространство, необходимое для db)

Ответ 10

Другой подход - это проблема всех пар с заданным порогом для некоторой функции подобия. Взгляните на фотоархив и код здесь http://code.google.com/p/google-all-pairs-similarity-search/

Я не знаю, соответствует ли ваша функция подобия подходу, но если это так, это еще один подход, на который нужно взглянуть. В любом случае это также потребует нормализованных и отсортированных векторов.