Разложение 3d-сетки в сетку 2d
Предположим, что у вас есть трехмерный объект, представленный как 3d-сетка в некотором распространенном формате. Как бы вы разработали алгоритм для декомпозиции сетки в одну или несколько 2d 'сетей? - то есть двумерное представление, которое можно вырезать и свернуть для создания исходного 3D-объекта.
Помимо всего прочего, алгоритм должен учитывать:
- Несколько возможных разложений для любого заданного объекта
- Обработка фитинга сетки в холсты фиксированного размера (листы бумаги).
- Признание того, что две панели в сети будут перекрываться (и, таким образом, недействительны).
- Разбиение сетки на несколько сетей, если они не могут быть представлены как один, из-за ограничений на перекрытие или размер страницы.
- Создание вкладок в соответствующих местах для прикрепления смежных граней.
Очевидным вырожденным случаем является просто создание одной сетки на лице с вкладками на половине ребер. Это не идеально, очевидно: идеальный случай представляет собой единую непрерывную сеть. Реальность для сложных фигур, вероятно, будет где-то посередине.
Я понимаю, что поиск оптимальной сети (наименьшее количество сетей/наименьших страниц), вероятно, является дорогостоящим вычислительным, но достаточной эвристикой для поиска сетей достаточно.
Ответы
Ответ 1
Когда я прочитал ваш вопрос, ко мне пришли слова "автоматический алгоритм бумажной печати". Таким образом, я искал его и нашел Модели Papercraft с использованием генерализованных цилиндров (pdf) от Massarwi и др.
Мы предлагаем новый метод для производства развернутые образцы округлые фигурки животных из триангулированные сетки с помощью полосковая аппроксимация. Хотя в принцип триангулированной модели может быть разворачивается просто за счет сохранения насколько возможно его подключение, в то время как проверка пересечения треугольников в развернутая плоскость, создающая узор с десятками тысяч треугольников нереально. Наш подход заключается в приблизить модель сетки набором непрерывные треугольные полосы без внутренние вершины. Первоначально мы подразделить нашу сетку на части соответствующих особенностям модель. Мы разделяем каждую часть на зональную регионов, группирующих треугольники, которые аналогичные топологические расстояния от часть границы. Мы генерируем треугольник с помощью упрощения сетки во время сохраняя границы зонального регионов и дополнительных разрезов. шаблон создается просто посредством разворачивая набор полос. отличительная особенность нашего метода состоит в том, что мы приближаем модель сетки набор непрерывных полос, а не другие линейчатые поверхности, такие как части конусов или цилиндров. Таким образом аппроксимированный развернутый рисунок может быть генерируется с использованием только операций с сеткой и простой алгоритм разворачивания. Кроме того, набор полосок может быть созданный только путем сгибания бумаги (без разрывов краев) и может представляют собой оригинальные модели сетки.
Существует также более ранняя связанная статья, называемая Модели бумажных ремесел из сеток (9MB pdf) Shatz et al.
В настоящем документе вводится алгоритм для сегментирование сетки в приближения. Алгоритм может быть используется в различных приложениях в САПР и компьютерной графики. Эта бумага основное внимание уделяется разработке и демонстрирует, что алгоритм генерирует приближения, которые может быть легко вырезан, и может быть склеены. Также показано, что ошибка между данной моделью и модель бумаги мала.
![enter image description here]()
Источник: http://www.ee.technion.ac.il/~ayellet/images/sel-papers-pic-5.jpg
Ответ 2
Алгоритмы eed3si9n, связанные с этим, будут генерировать хорошие разумные сетки сплетения из сложной геометрии. Если вы хотите развернуть сетку точно так же, как она смоделирована, например, для моделей с многогранниками, то здесь достаточно простой метод разворачивания любой сетки, поскольку она стоит
Построить граф из исходной сетки, где каждая грань является вершиной в графе, а две вершины связаны, если они имеют общий ребро в сетке. Один из этих графиков представляет собой разворачиваемую сетку тогда и только тогда, когда она не имеет циклов, т.е. Является деревом.
Хорошее дерево представляет собой наименьшее количество линий сгиба, чтобы добраться до самого дальнего лица от начальной точки, так как каждая сводка представляет собой ошибку, которая будет накапливаться в готовой модели. Алгоритм Дейкстры хорош здесь, но минимальное остовное дерево не работает. С каждым весом, равным весу, все деревья являются минимальными связующими деревьями, даже один, который разворачивает вашу сетку в одну большую спираль. Когда вы склеиваете модель вместе, ошибки будут возникать до тех пор, пока последние несколько лиц не подходят вообще.
Когда у вас есть дерево, начните с рисования стартового лица в начале координат. Затем пройдите по дереву и добавьте новые грани, вычислив новую вершину как пересечение двух окружностей с радиусами, соответствующими длине ребер в исходной сетке. Места для вкладок соответствуют краям, которые были в исходной сетке, но не находятся в плоском дереве.
Пользовательские разрезы могут обрабатываться как удаленные края перед шагом дерева.
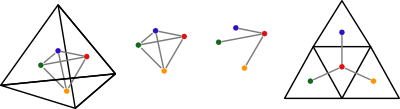
![diagram of unfolding a tetrahedron]()
Некоторые недостатки этой техники заключаются в том, что она будет счастливо создавать перекрывающиеся части в плоском шаблоне, и это зависит от поиска хорошего начального лица. Я попробовал Флойда-Варшаля найти лицо с минимальным диаметром, чтобы начать с него, но его поведение O (n ^ 3) было сделано для чрезмерно длительных перерывов в кофе. С перекрывающимися частями можно было бы разметить эту ветвь дерева как "неполную", пропустить ее и снова запустить алгоритм на всех неполных лицах.
Ответ 3
Я знаю, что это не ответ, но это связано. Ex-SGI графический парень Paul Haeberli Lamina программа является решением этой проблемы.