Как программист, как бы вы объяснили мнимые числа?
Как программист, я считаю, что моя работа - быть хорошей математикой, но у меня возникают проблемы с моей головой вокруг воображаемых чисел. Я попробовал google и wikipedia без везения, поэтому я надеюсь, что программист сможет мне объяснить, дайте мне пример номера квадрат, который равен <= 0, пример использования примера и т.д.
Ответы
Ответ 1
Я предполагаю, что это является одним из хороших объяснений:
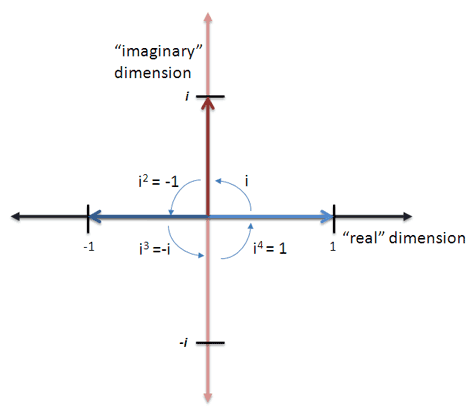
Ключевое слово вращение (в отличие от direction для отрицательных чисел, которые столь же странны, как и мнимые числа, когда вы думаете о них: меньше, чем ничего?)
![alt text]()
Как отклонение модели отрицательных чисел, мнимые числа могут моделировать все, что вращается между двумя измерениями "X" и "Y" . Или что-нибудь с циклической, круговой связью
Ответ 2
Проблема: я не просто программист, я математик.
Решение: все равно плуг.
Там нет ничего магического для сложных чисел. Идея их создания заключается в том, что с реальными числами что-то не так. Если у вас есть уравнение x ^ 2 + 4, это никогда не равно нулю, тогда как x ^ 2 - 2 равно нулю дважды. Итак, математики действительно разозлились и хотели, чтобы там всегда были нули с полиномами степени по крайней мере один (требуется "алгебраически замкнутое" поле) и создали некоторое произвольное число j такое, что j = sqrt (-1). Все правила отходят от места (хотя они более точно реорганизуются по-разному - в частности, вы формально не можете сказать "эй, это число является квадратным корнем отрицательного" ). Если это число j, вы можете получить кратность j. И вы можете добавить реальные числа в j, поэтому у вас есть сложные числа. Операции с комплексными числами аналогичны операциям с биномами (преднамеренно).
Реальная проблема с комплексами заключается не во всем этом, а в том, что вы не можете определить систему, посредством которой вы можете получить обычные правила для меньшего и большего. Так что, вы попадаете туда, где вы вообще не определяете его. Это не имеет смысла в двумерном пространстве. Поэтому, честно говоря, я не могу ответить "дайте мне число квадратов чисел, которое равно <= 0", хотя "j" имеет смысл, если вы рассматриваете его квадрат как действительное число, а не комплексное число.
Что касается применений, я лично использовал их больше всего при работе с фракталами. Идея фрактала мандельброта состоит в том, что он является способом графического отображения z = z ^ 2 + c и его расходимости вдоль вещественных мнимых осей.
Ответ 3
Вы также можете спросить, почему существуют отрицательные числа? Они существуют, потому что вы хотите представить решения для некоторых уравнений типа: x + 5 = 0. То же самое относится и к мнимым числам, вы хотите компактно представить решения уравнений вида: x ^ 2 + 1 = 0.
Вот один из способов, которым я видел их на практике. В EE вы часто имеете дело с функциями, которые являются синусоидальными волнами или которые могут быть разложены на синусоидальные волны. (См. Например Серия Фурье).
Следовательно, вы часто увидите решения уравнений вида:
f (t) = A * cos (wt)
Кроме того, часто вы хотите представлять функции, которые по какой-либо фазе сдвигаются из этой функции. Фазовый сдвиг на 90 градусов даст вам функцию sin.
g (t) = B * sin (wt)
Вы можете получить произвольный фазовый сдвиг, объединив эти две функции (называемые синфазными и квадратурными компонентами).
h (t) = Acos (wt) + iB * sin (wt)
Ключевым моментом здесь является то, что в линейной системе: если f (t) и g (t) решают уравнение, h (t) также решает одно и то же уравнение. Итак, теперь мы имеем общее решение уравнения h (t).
Хорошая вещь о h (t) состоит в том, что ее можно записать компактно как
h (t) = Cexp (wt + theta)
Используя тот факт, что exp (iw) = cos (w) + я * sin (w).
В этом нет ничего необычайно глубокого. Это просто использование математической идентичности для компактного представления общего решения широкого круга уравнений.
Ответ 4
Ну, для программиста:
class complex {
public:
double real;
double imaginary;
complex(double a_real) : real(a_real), imaginary(0.0) { }
complex(double a_real, double a_imaginary) : real(a_real), imaginary(a_imaginary) { }
complex operator+(const complex &other) {
return complex(
real + other.real,
imaginary + other.imaginary);
}
complex operator*(const complex &other) {
return complex(
real*other.real - imaginary*other.imaginary,
real*other.imaginary + imaginary*other.real);
}
bool operator==(const complex &other) {
return (real == other.real) && (imaginary == other.imaginary);
}
};
Что в принципе все есть. Сложные числа - это только пары действительных чисел, для которых определены особые перегрузки +, * и ==. И эти операции действительно просто определяются так. Тогда оказывается, что эти пары чисел с этими операциями хорошо вписываются в остальную математику, поэтому они получают специальное имя.
Это не так много чисел, как в "подсчете", но больше похоже на "можно манипулировать с помощью +, -, *,... и не вызывать проблем при смешивании с" обычными "числами". Они важны, потому что они заполняют дыры, оставленные действительными числами, например, что нет номера, имеющего квадрат -1. Теперь у вас есть complex(0, 1) * complex(0, 1) == -1.0, который является полезной нотацией, так как вам больше не нужно обрабатывать отрицательные числа в этих случаях. (И, как выясняется, в основном все остальные специальные случаи больше не нужны, когда вы используете комплексные числа)
Ответ 5
Если вопрос: "Существуют ли мнимые числа?" или "Как существуют мнимые числа?" то это не вопрос для программиста. Это может быть даже не вопросом для математика, а скорее метафизиком или философом математики, хотя математик может почувствовать необходимость оправдать свое существование в этой области. Полезно начать с обсуждения того, как существуют числа (довольно много математиков, которые подошли к этому вопросу, - это платоники, фии). Некоторые настаивают на том, что мнимые числа (как это делал ранний Уайтхед) - практическое удобство. Но тогда, если мнимые числа являются просто практическим удобством, что это говорит о математике? Вы не можете просто объяснить мнимые числа как простой практический инструмент или пару действительных чисел без учета обеих пар, а общие последствия их "практического". Другие настаивают на существовании мнимых чисел, утверждая, что их небытие подрывает физические теории, которые их сильно используют (QM колено в сложных гильбертовых пространствах). Я полагаю, что проблема выходит за рамки этого веб-сайта.
Если ваш вопрос намного больше, чем на землю, например. как выражать мнимые числа в программном обеспечении, тогда ответ выше (пара реалов вместе с определенными операциями из них).
Ответ 6
Главное, что вы добавляете числа, которые вы define должны быть решениями квадратичных уравнений, таких как x 2= -1. Назовите одно решение этого уравнения i, затем из этого уравнения следуют правила вычисления для i.
Это похоже на определение отрицательных чисел как решение уравнений типа 2 + x = 1, когда вы знали только положительные числа или фракции как решения уравнений типа 2x = 1, когда вы знали только целые числа.
Ответ 7
Лучше всего перестать пытаться понять, как число может быть квадратным корнем из отрицательного числа, и просто продолжайте с предположения, что это так.
Итак (используя я в качестве квадратного корня из -1):
(3+5i)*(2-i)
= (3+5i)*2 + (3+5i)*(-i)
= 6 + 10i -3i - 5i * i
= 6 + (10 -3)*i - 5 * (-1)
= 6 + 7i + 5
= 11 + 7i
работает в соответствии со стандартными правилами математики (помня, что я квадрат равен -1 в строке 4).
Ответ 8
Мнимое число - это действительное число, умноженное на мнимую единицу i. i определяется как:
i == sqrt(-1)
Итак:
i * i == -1
Используя это определение, вы можете получить квадратный корень из отрицательного числа следующим образом:
sqrt(-3)
== sqrt(3 * -1)
== sqrt(3 * i * i) // Replace '-1' with 'i squared'
== sqrt(3) * i // Square root of 'i squared' is 'i' so move it out of sqrt()
И ваш окончательный ответ - действительное число sqrt(3), умноженное на мнимую единицу i.
Ответ 9
Короткий ответ: реальные числа являются одномерными, мнимые числа добавляют второе измерение к уравнению, и некоторые странные вещи случаются, если вы умножаете...
Ответ 10
Если вам интересно найти простое приложение и если вы знакомы с матрицами,
иногда полезно использовать комплексные числа, чтобы преобразовать совершенно реальную матрицу в треугольную в сложном пространстве, и это упрощает вычисление на ней.
Результат, конечно, совершенно реальный.
Ответ 11
Отличные ответы до сих пор (действительно, как Девин!)
Еще одна точка:
Одно из первых применений комплексных чисел (хотя в то время они не назывались таким образом) было промежуточным шагом в решении уравнений третьей степени.
ссылка
Опять же, это чисто инструмент, который используется для ответа на реальные проблемы с реальными числами, имеющими физический смысл.
Ответ 12
Я не хочу превращать этот сайт в переполнение математики, но для тех, кто интересуется: посмотрите "Воображаемая история: история sqrt (-1)" Пол Дж. Нахина. Он рассказывает о всей истории и различных приложениях воображаемых чисел веселым и захватывающим образом. Эта книга сделала то, что я решил закончить математику, когда прочитал ее 7 лет назад (и я думал о искусстве). Отлично читаю.
Ответ 13
В электротехнике импеданс Z индуктора равен jwL, где w = 2 * pi * f (частота) и j (sqrt (-1)) означает, что он ведет на 90 градусов, а для конденсатора Z = 1/jwc = -j/wc, что составляет -90deg/wc, так что он отстает от простого резистора на 90 градусов.