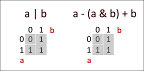
Почему (a | b) эквивалентно a - (a & b) + b?
Я искал способ сделать BITOR() с базой данных Oracle и наткнулся на предложение просто использовать BITAND() вместо этого, заменив BITOR (a, b) на + b - BITAND (a, b).
Я тестировал его вручную несколько раз и проверял, что он работает для всех двоичных чисел, о которых я мог думать, но я не могу придумать быстрое математическое доказательство того, почему это правильно.
Может ли кто-нибудь просветить меня?
Ответы
Ответ 1
A и B - это набор бит, которые включены как в A, так и в B. A - (A и B) оставляет вас со всеми этими битами, которые находятся только в A. Добавьте B к этому, и вы получите все бит, которые включены в или те, которые включены в B.
Простое добавление A и B не будет работать из-за переноса, где оба имеют 1 бит. Сначала удаляя биты, общие для A и B, мы знаем, что (A- (A & B)) не будет иметь битов, общих с B, поэтому их объединение гарантировано не приведет к переносу.
Ответ 2
Представьте, что у вас есть два двоичных числа: a и b. И пусть говорят, что эти числа никогда не имеют 1 в одном бите в одно и то же время, то есть если a имеет 1 в некотором бите, b всегда имеет 0 в соответствующем бите. И в другом направлении, если b имеет 1 в некотором разряде, тогда a всегда имеет 0 в этом бите. Например
a = 00100011
b = 11000100
Это будет пример a и b, удовлетворяющий указанному выше условию. В этом случае легко видеть, что a | b будет точно таким же, как a + b.
a | b = 11100111
a + b = 11100111
Теперь возьмем два числа, которые нарушают наше условие, т.е. два числа имеют по крайней мере один 1 в некотором общем бите
a = 00100111
b = 11000100
Является ли a | b таким же, как a + b в этом случае? Нет
a | b = 11100111
a + b = 11101011
Почему они разные? Они различны, потому что, когда мы + бит, который имеет 1 в обоих числах, мы создаем так называемый перенос: результирующий бит равен 0, а 1 переносится на следующий бит влево: 1 + 1 = 10. Операция | не переносится, поэтому 1 | 1 снова просто 1.
Это означает, что разница между a | b и a + b происходит тогда и только тогда, когда числа имеют как минимум один общий бит. Когда мы суммируем два числа с 1 общим битом, эти общие биты добавляются "дважды" и производят перенос, который разрушает сходство между a | b и a + b.
Теперь посмотрим на a & b. Что вычисляет a & b? a & b выводит число, которое имеет 1 во всех битах, где оба a и b имеют 1. В нашем последнем примере
a = 00100111
b = 11000100
a & b = 00000100
Как вы видели выше, это именно те биты, которые делают a + b отличаться от a | b. 1 в a & b указывает все позиции, в которых будет происходить перенос.
Теперь, когда мы делаем a - (a & b), мы эффективно удаляем (вычитаем) все "оскорбительные" биты из a и только такие биты
a - (a & b) = 00100011
Числа a - (a & b) и b не имеют общих 1 бит, что означает, что если мы добавим a - (a & b) и b, мы не столкнемся с переносом, и, если вы думаете об этом, мы должны закончить с таким же результатом, как если бы мы просто сделали a | b
a - (a & b) + b = 11100111
Ответ 3
A & B = C, где любые биты, оставленные в C, заданы как в A, так и в B.
Либо A-C = D, либо B-C = E устанавливает только эти общие биты в 0. Несущий эффект отсутствует, поскольку 1-1 = 0.
D + B или E + A аналогичен A + B, за исключением того, что, поскольку мы вычитали A & B ранее, не будет переноса, поскольку он очистил все обычно установленные биты в D или E.
Конечным результатом является то, что A-A & B + B или B-A & B + A эквивалентно A | B.
Здесь таблица истинности, если она все еще запутывает:
A | B | OR A | B | & A | B | - A | B | +
---+---+---- ---+---+--- ---+---+--- ---+---+---
0 | 0 | 0 0 | 0 | 0 0 | 0 | 0 0 | 0 | 0
0 | 1 | 1 0 | 1 | 0 0 | 1 | 0-1 0 | 1 | 1
1 | 0 | 1 1 | 0 | 0 1 | 0 | 1 1 | 0 | 1
1 | 1 | 1 1 | 1 | 1 1 | 1 | 0 1 | 1 | 1+1
Обратите внимание на строки переноса в операциях + и - мы избегаем тех, которые, поскольку A- (A & B) задают случаи, оба бита в и B от 1 до 0 в A, а затем добавление их из B также приводит к в других случаях было 1 в или B, но не там, где оба имели 0, поэтому таблица истинности OR и таблица истинности A- (A & B) + B идентичны.
Другим способом глазного яблока является видеть, что A + B почти похож на A | B, за исключением переноса в нижнем ряду. A & B выделяет, что нижний ряд для нас, A-A & B перемещает те изолированные изолированные в две строки в таблице +, и (A-A & B) + B становится эквивалентным A | B.
Пока вы могли бы коммутировать это с A + B- (A & B), я боялся возможного переполнения, но это было неоправданно:
#include <stdio.h>
int main(){ unsigned int a=0xC0000000, b=0xA0000000;
printf("%x %x %x %x\n",a, b, a|b, a&b);
printf("%x %x %x %x\n",a+b, a-(a&b), a-(a&b)+b, a+b-(a&b)); }
c0000000 a0000000 e0000000 80000000
60000000 40000000 e0000000 e0000000
Изменить: поэтому я написал это до того, как были ответы, а затем на мой домашний контакт было около двух часов, и мне, наконец, удалось опубликовать его, заметив только после этого, что он был правильно ответил дважды. Лично я предпочитаю ссылаться на таблицу истинности для выработки побитовых операций, поэтому я оставлю ее на случай, если она кому-то поможет.
Ответ 4
![stackoverflow_answer_1604258_why-is-a-b-equivalent-to-a-a-b-b.png]()