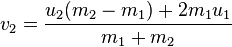Болт-коллаж - обнаружение и обработка

Ответ 1

Чтобы определить, сталкиваются ли два шара, просто проверьте, меньше ли расстояние между их центрами меньше радиуса. Чтобы сделать совершенно упругое столкновение между шарами, вам нужно только беспокоиться о компоненте скорости, которая находится в направлении столкновения. Другой компонент (касательный к столкновению) останется неизменным для обоих шаров. Вы можете получить компоненты столкновения, создав единичный вектор, указывающий в направлении от одного шара к другому, а затем возьмем точечный продукт с векторами скорости шаров. Затем вы можете подключить эти компоненты в одномерное упругое уравнение столкновения.

В Википедии есть довольно хорошая сводка всего процесса. Для шаров любой массы новые скорости могут быть вычислены с использованием уравнений (где v1 и v2 - скорости после столкновения, а u1, u2 - из ранее):

Если шары имеют одинаковую массу, то скорости просто переключаются. Вот код, который я написал, который делает что-то подобное:

void Simulation::collide(Storage::Iterator a, Storage::Iterator b)
{
    // Check whether there actually was a collision
    if (a == b)
        return;

    Vector collision = a.position() - b.position();
    double distance = collision.length();
    if (distance == 0.0) {              // hack to avoid div by zero
        collision = Vector(1.0, 0.0);
        distance = 1.0;
    }
    if (distance > 1.0)
        return;

    // Get the components of the velocity vectors which are parallel to the collision.
    // The perpendicular component remains the same for both fish
    collision = collision / distance;
    double aci = a.velocity().dot(collision);
    double bci = b.velocity().dot(collision);

    // Solve for the new velocities using the 1-dimensional elastic collision equations.
    // Turns out it really simple when the masses are the same.
    double acf = bci;
    double bcf = aci;

    // Replace the collision velocity components with the new ones
    a.velocity() += (acf - aci) * collision;
    b.velocity() += (bcf - bci) * collision;
}

Что касается эффективности, Райан Фокс прав, вы должны рассмотреть вопрос о разделении региона на разделы, а затем выполнить обнаружение столкновений в каждом разделе. Имейте в виду, что шары могут сталкиваться с другими шарами на границах раздела, поэтому это может сделать ваш код намного сложнее. Эффективность, вероятно, не будет иметь значения, пока у вас не будет несколько сотен мячей. Для бонусных очков вы можете запускать каждый раздел на другом ядре или разбивать обработку столкновений в каждом разделе.

Ответ 2

Хорошо, много лет назад я сделал программу, как вы здесь. Существует одна скрытая проблема (или многие, зависит от точки зрения):

• Если скорость мяча тоже высоко, вы можете пропустить столкновение.

А также почти в 100% случаях ваши новые скорости будут неправильными. Ну, не скорости, а позиции. Вы должны рассчитывать новые скорости точно в нужном месте. В противном случае вы просто сбрасываете шары на небольшое количество "ошибок", которое доступно на предыдущем дискретном шаге.

Решение очевиден: вам нужно разделить временную метку так, чтобы сначала вы переместились в правильное место, затем столкнулись, а затем переместились на оставшееся время.

Ответ 3

Для решения этой проблемы необходимо использовать разметку пространства.

Читайте дальше Двоичное пространственное разделение а также Квадраты

Ответ 4

В качестве пояснения к предложению Райана Фокса разделить экран на регионы и проверить только столкновения внутри регионов...

например. разделить зону воспроизведения вверх на сетку квадратов (которая будет произвольно произносить 1 единицу длины на каждую сторону) и проверить наличие столкновений внутри каждого квадрата сетки.

Это абсолютно правильное решение. Единственная проблема с ним (как указывал еще один плакат) состоит в том, что столкновения между границами являются проблемой.

Решением этого является наложение второй сетки с вертикальным и горизонтальным смещением на 0,5 единицы к первому.

Тогда любые столкновения, которые будут пересекаться через границы в первой сетке (и, следовательно, не обнаружены), будут находиться внутри квадратов сетки во второй сетке. Пока вы отслеживаете столкновения, с которыми вы уже справились (поскольку, вероятно, будет некоторое перекрытие), вам не нужно беспокоиться о том, как обращаться с крайними случаями. Все столкновения будут находиться в квадрате сетки на одной из сеток.

Ответ 5

Хорошим способом сокращения числа проверок столкновения является разделение экрана на разные разделы. Затем вы сравниваете каждый шар с шарами в том же разделе.

Ответ 6

Одна вещь, которую я вижу здесь, чтобы оптимизировать.

Пока я согласен, что шары попадают, когда расстояние является суммой их радиусов, никогда не следует рассчитывать на это расстояние! Скорее, вычислите его квадрат и работайте с ним таким образом. Нет причин для этой дорогостоящей операции с квадратным корнем.

Кроме того, как только вы обнаружили столкновение, вы должны продолжать оценивать столкновения, пока не останется больше. Проблема в том, что первый может заставить других решить проблему, прежде чем вы получите точную картину. Подумайте, что произойдет, если мяч попадает в мяч по краю? Второй мяч попадает в край и сразу же подбирается к первому мячу. Если вы стучите в кучу мячей в углу, вы можете столкнуться с несколькими столкновениями, которые должны быть решены, прежде чем вы сможете повторять следующий цикл.

Что касается O (n ^ 2), все, что вы можете сделать, это свести к минимуму затраты на отказ от пропущенных:

1) Мяч, который не движется, не может ничего ударить. Если на полу есть разумное количество мячей, это может сэкономить много испытаний. (Обратите внимание, что вы все равно должны проверить, попало ли что-то в неподвижный мяч.)

2) Что-то, что может стоить сделать: Разделите экран на несколько зон, но линии должны быть нечеткими - шары на краю зоны перечислены как находящиеся во всех соответствующих (может быть 4) зонах. Я бы использовал сетку 4x4, сохраняя зоны как биты. Если И из зон двух зон шариков возвращает ноль, конец теста.

3) Как я уже говорил, не делайте квадратный корень.

Ответ 7

Я нашел отличную страницу с информацией об обнаружении и ответе на столкновение в 2D.

http://www.metanetsoftware.com/technique.html

Они пытаются объяснить, как это делается с академической точки зрения. Они начинаются с простого обнаружения столкновения объектов с объектом, и переходят к ответу на столкновение и как его масштабировать.

Изменить: Обновлена ​​ссылка

Ответ 8

У вас есть два простых способа сделать это. Джей закрыл точный способ проверки из центра мяча.

Более простой способ - использовать прямоугольный ограничивающий прямоугольник, установить размер вашего поля на 80% по размеру мяча, и вы будете хорошо имитировать столкновение.

Добавьте метод к вашему классу шаров:

public Rectangle getBoundingRect()
{
   int ballHeight = (int)Ball.Height * 0.80f;
   int ballWidth = (int)Ball.Width * 0.80f;
   int x = Ball.X - ballWidth / 2;
   int y = Ball.Y - ballHeight / 2;

   return new Rectangle(x,y,ballHeight,ballWidth);
}

Затем в вашем цикле:

// Checks every ball against every other ball. 
// For best results, split it into quadrants like Ryan suggested. 
// I didn't do that for simplicity here.
for (int i = 0; i < balls.count; i++)
{
    Rectangle r1 = balls[i].getBoundingRect();

    for (int k = 0; k < balls.count; k++)
    {

        if (balls[i] != balls[k])
        {
            Rectangle r2 = balls[k].getBoundingRect();

            if (r1.Intersects(r2))
            {
                 // balls[i] collided with balls[k]
            }
        }
    }
}

Ответ 9

Я вижу, что он намекнул здесь и там, но сначала вы можете выполнить более быстрый расчет, например, сравнить ограничивающие поля для перекрытия, а THEN выполнить перекрытие по радиусу, если этот первый тест пройдет.

Математика сложения/разности намного быстрее для ограничивающего прямоугольника, чем все тригг для радиуса, и в большинстве случаев тест с ограничивающей рамкой отклоняет возможность столкновения. Но если вы повторите тест с помощью триггера, вы получите точные результаты, которые вы ищете.

Да, это два теста, но они будут быстрее в целом.

Ответ 10

Этот KineticModel является реализацией цитированного в Java.

Ответ 11

Я реализовал этот код в JavaScript с помощью элемента HTML Canvas, и он произвел замечательные симуляции со скоростью 60 кадров в секунду. Я начал моделирование с помощью коллекции из десятка шариков в случайных положениях и скоростях. Я обнаружил, что при более высоких скоростях кратковременное столкновение между маленьким шаром и намного большим заставляло маленький шар казаться STICK к краю большего шара и перемещался примерно до 90 градусов вокруг большой шар перед отделением. (Интересно, заметил ли кто-нибудь еще такое поведение.)

Некоторые протоколирования вычислений показали, что минимальное количество переводов в этих случаях было недостаточно большим, чтобы предотвратить одновременное слияние шаров на следующем шаге. Я экспериментировал и обнаружил, что могу решить эту проблему, увеличив MTD на основе относительных скоростей:

dot_velocity = ball_1.velocity.dot(ball_2.velocity);
mtd_factor = 1. + 0.5 * Math.abs(dot_velocity * Math.sin(collision_angle));
mtd.multplyScalar(mtd_factor);

Я проверил, что до и после этого исправления полная кинетическая энергия сохранялась для каждого столкновения. Значение 0.5 в mtd_factor было примерно равным минимальному значению, которое всегда заставляло шары разделиться после столкновения.

Хотя это исправление вводит небольшую ошибку в точной физике системы, компромисс заключается в том, что теперь очень быстрые шары могут быть смоделированы в браузере без уменьшения размера временного шага.

Ответ 12

Как я вижу здесь, лучший способ его реализации не упоминается. Я расскажу вам "Как имитировать бильярд и Похожие системы" Бориса Д. Любачевского, доступного по arxiv: http://arxiv.org/abs/cond-mat/0503627 На прилагаемом рисунке показан снимок экрана программы, которую я намереваюсь сделать с открытым исходным кодом, когда я закончу его. Даже на ранней стадии он работает с 5000 шарами довольно гладко. Надеюсь, это будет еще лучше, хотя я не хочу внедрять секционирование, я хочу, чтобы код был понятен. Описание будет доступно на http://compphys.go.ro

Далее отредактируйте: Код теперь доступен на GitHub: https://github.com/aromanro/EventMolecularDynamics Описание находится в блоге: http://compphys.go.ro/event-driven-molecular-dynamics/