Ответ 1
В моей неудачной попытке нарисовать здесь порядок, который показывает, как их следует выбирать.

в значительной степени выберите node, который находится непосредственно над строкой.
У меня есть следующий текст из академического курса, который я взял некоторое время назад об обходном порядке (они также называют его pancaking) двоичного дерева (не BST):
Обход дерева порядка
Нарисуйте линию вокруг дерево. Начните с левой стороны от корня, и обойти вокруг дерева, чтобы закончить до корня. Оставайтесь как можно ближе к дереву, но не пересекают дерево. (Думать о дерево - его ветки и узлы - как твердый барьер.) Порядок узлы - это порядок, в котором эта строка проходит под ними. Если ты неуверенный относительно того, когда вы идете "под" a node, помните, что a node "для слева" всегда на первом месте.
Здесь используется пример (немного другое дерево ниже)
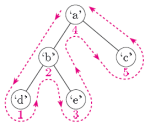
Однако, когда я выполняю поиск в google, я получаю противоречивое определение. Например, пример википедии:
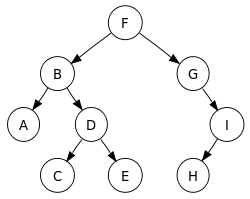
Последовательность обхода порядка: A, B, C, D, E, F, G, H, я (левый, корневой, правый node)
Но согласно (моему пониманию) определения № 1 это должно быть
A, B, D, C, E, F, G, I, H
Может ли кто-нибудь уточнить, какое определение верно? Они могут описывать разные методы обхода, но, случается, используют одно и то же имя. У меня возникают проблемы с тем, что рецензируемый академический текст неверен, но не может быть уверен.
В моей неудачной попытке нарисовать здесь порядок, который показывает, как их следует выбирать.

в значительной степени выберите node, который находится непосредственно над строкой.
Забудьте определения, гораздо проще применить алгоритм:
void inOrderPrint(Node root)
{
if (root.left != null) inOrderPrint(root.left);
print(root.name);
if (root.right != null) inOrderPrint(root.right);
}
Это всего три строки. Переупорядочить порядок пред- и пост-заказа.
Если вы внимательно прочитаете, вы увидите, что первое "определение" говорит о начале слева от корня и что порядок узлов определяется, когда вы проходите под ними. Итак, B не первый node, так как вы передаете его слева на пути к A, затем сначала проходите под A, после чего вы поднимаетесь и проходите под B. Поэтому кажется, что оба определения дают одинаковый результат.
Я лично нашел эту лекцию весьма полезной.
Оба определения дают одинаковый результат. Не обманывайте буквы в первом примере - посмотрите на цифры по пути. Второй пример использует буквы для обозначения пути - возможно, это то, что отбрасывает вас.
Например, в вашем примере, показывающем, как вы считали, что второе дерево будет пройдено с использованием алгоритма первого, вы помещаете "D" после "B", но вы не должны, потому что по-прежнему остается левая существует дочерний node из D (поэтому первый элемент говорит "порядок, в котором эта строка проходит под".
Я думаю, что первое двоичное дерево с корнем a является двоичным деревом, которое неправильно построено.
Попробуйте реализовать так, чтобы вся левая часть дерева была меньше корня, а вся правая часть дерева больше или равна корню.
это может быть поздно, но это может быть полезно для всех позже. u просто не нужно игнорировать фиктивные или нулевые узлы, например, Node G имеет левый нуль Node.., учитывая, что этот null Node сделает все хорошо.
Правильный обход будет: насколько это возможно, с листовыми узлами (не корневыми узлами)
F является корнем или левым, я не уверен
Но согласно (моему пониманию) определение # 1, это должно быть
A, B, D, C, E, F, G, I, H
К сожалению, ваше понимание неверно.
Всякий раз, когда вы приходите к node, вы должны спуститься до доступного левого node, прежде чем смотреть на текущий node, тогда вы посмотрите на доступное право node. Когда вы выбрали D до C, вы сначала не спустились влево node.
Эй, согласно мне, как упоминалось в wiki, правильная последовательность для обходного порядка слева-root-right.
До A, B, C, D, E, F, я думаю, вы уже поняли. Теперь после root F следующий node - это G, который не имеет левой node, а правый node, так как в соответствии с правилом (left-root-right) его null-g-right. Теперь я правильный node для G, но у меня есть левый node, следовательно, обход будет GHI. Это правильно.
Надеюсь, что это поможет.
Для обходного пути по дереву вы должны иметь в виду, что порядок обхода оставлен - node -right. Для приведенной выше диаграммы, в которой вы столкнулись, ваша ошибка возникает, когда вы читаете родительский node, прежде чем читать какие-либо листовые (дочерние) узлы слева.
Правильный обход будет: насколько это возможно, с листовыми узлами (A), вернитесь к родительскому node (B), переместитесь вправо, но так как D имеет дочерний элемент слева от него, вы снова перемещаетесь ( C), вернитесь к родительскому элементу C (D), к D правильному ребенку (E), вернитесь назад к корню (F), перейдите в правый лист (G), перейдите к G leaf, но так как он имеет левый лист node переместите туда (H), вернитесь к родительскому (I).
приведенный выше обход читает node, когда я его перечисляю в скобках.
пакетная структура данных;
открытый класс BinaryTreeTraversal {
public static Node<Integer> node;
public static Node<Integer> sortedArrayToBST(int arr[], int start, int end) {
if (start > end)
return null;
int mid = start + (end - start) / 2;
Node<Integer> node = new Node<Integer>();
node.setValue(arr[mid]);
node.left = sortedArrayToBST(arr, start, mid - 1);
node.right = sortedArrayToBST(arr, mid + 1, end);
return node;
}
public static void main(String[] args) {
int[] test = new int[] { 1, 2, 3, 4, 5, 6, 7 };
Node<Integer> node = sortedArrayToBST(test, 0, test.length - 1);
System.out.println("preOrderTraversal >> ");
preOrderTraversal(node);
System.out.println("");
System.out.println("inOrderTraversal >> ");
inOrderTraversal(node);
System.out.println("");
System.out.println("postOrderTraversal >> ");
postOrderTraversal(node);
}
public static void preOrderTraversal(Node<Integer> node) {
if (node != null) {
System.out.print(" " + node.toString());
preOrderTraversal(node.left);
preOrderTraversal(node.right);
}
}
public static void inOrderTraversal(Node<Integer> node) {
if (node != null) {
inOrderTraversal(node.left);
System.out.print(" " + node.toString());
inOrderTraversal(node.right);
}
}
public static void postOrderTraversal(Node<Integer> node) {
if (node != null) {
postOrderTraversal(node.left);
postOrderTraversal(node.right);
System.out.print(" " + node.toString());
}
}
}
пакетная структура данных;
public class Node {
E value = null;
Node<E> left;
Node<E> right;
public E getValue() {
return value;
}
public void setValue(E value) {
this.value = value;
}
public Node<E> getLeft() {
return left;
}
public void setLeft(Node<E> left) {
this.left = left;
}
public Node<E> getRight() {
return right;
}
public void setRight(Node<E> right) {
this.right = right;
}
@Override
public String toString() {
return " " +value;
}
}
preOrderTraversal → 4 2 1 3 6 5 7 inOrderTraversal → 1 2 3 4 5 6 7 postOrderTraversal → 1 3 2 5 7 6 4
void
inorder (NODE root)
{
if (root != NULL)
{
inorder (root->llink);
printf ("%d\t", root->info);
inorder (root->rlink);
}
}
Это самый простой подход к рекурсивному определению обхода в порядке, просто вызовите эту функцию в основной функции, чтобы получить обход в порядке заданного двоичного дерева.
Это правильно для preorder, nt для inorder