Ответ 1
Короткий ответ
Пул chunksize-алгоритм является эвристическим. Он предоставляет простое решение для всех возможных проблемных сценариев, которые вы пытаетесь внедрить в методы пула. Как следствие, он не может быть оптимизирован для какого-либо конкретного сценария.
Алгоритм произвольно делит итерируемое примерно на четыре раза больше фрагментов, чем наивный подход. Чем больше блоков, тем больше накладных расходов, но повышается гибкость планирования. Как этот ответ покажет, это приводит к более высокой загрузке работника в среднем, но без гарантии более короткого общего времени вычислений для каждого случая.
"Приятно знать, - подумаете вы, - но как знание этого помогает мне в решении конкретных проблем с многопроцессорностью?" Ну, это не так. Более честный короткий ответ: "короткого ответа нет", "многопроцессорная обработка сложна" и "это зависит". Наблюдаемый симптом может иметь разные корни даже для сходных сценариев.
Этот ответ пытается дать вам базовые понятия, помогающие получить более четкое представление о черном ящике планирования пула. Он также пытается дать вам некоторые базовые инструменты для распознавания и предотвращения потенциальных обрывов, поскольку они связаны с размером кусков.
Оглавление
Часть I
- Определения
- Цели распараллеливания
- Сценарии распараллеливания
- Риски Chunksize> 1
- Пул Chunksize-Алгоритм
Количественная оценка эффективности алгоритма
6.1 Модели
6.2 Параллельное расписание
6.3 Эффективность
6.3.1 Абсолютная эффективность распределения (ADE)
6.3.2 Относительная эффективность распределения (RDE)
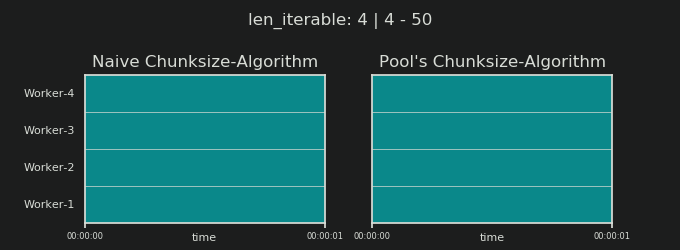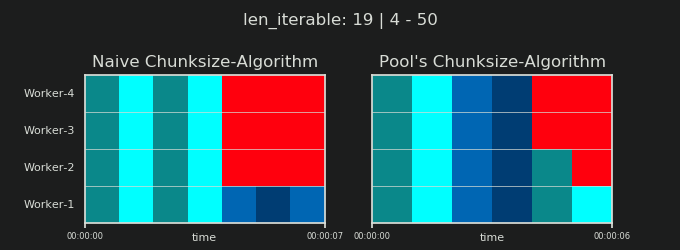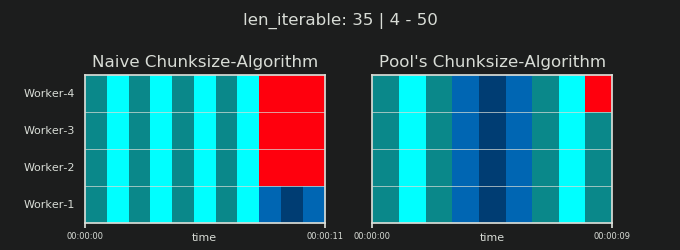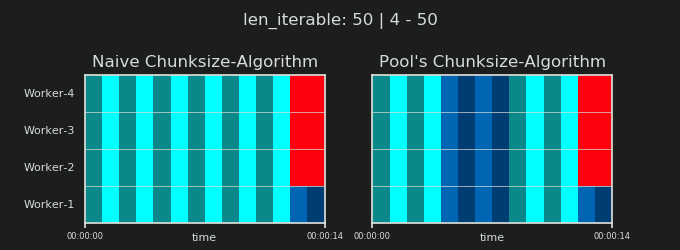
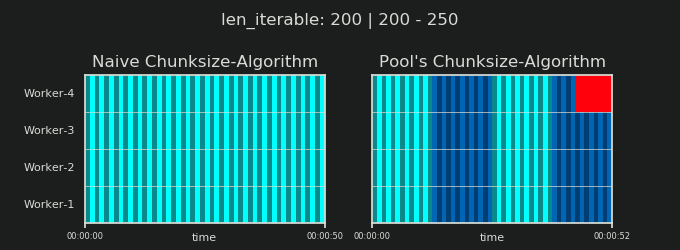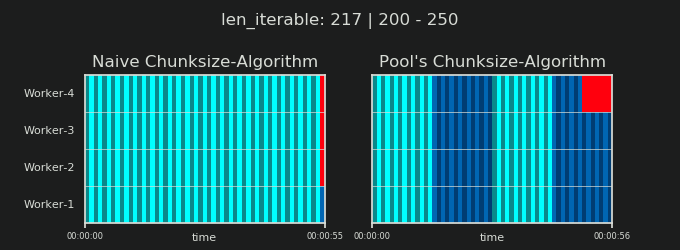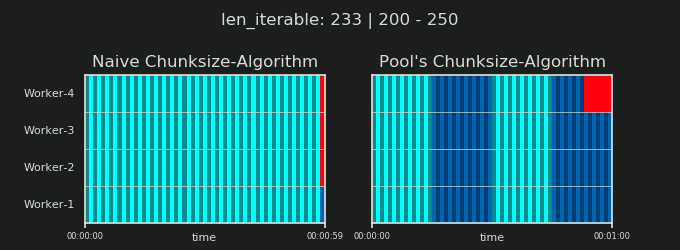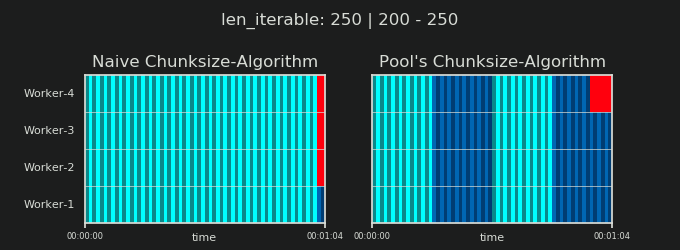
- Наивный и пул Chunksize-Алгоритм
- Проверка на практике
- Заключение
Сначала необходимо уточнить некоторые важные термины.
1. Определения
ломоть
Чанк здесь - это доля iterable -argument, указанного в вызове пула -method. Как вычисляется размер фрагмента и как это может повлиять, - тема этого ответа.
задача
Физическое представление задачи в рабочем процессе в терминах данных можно увидеть на рисунке ниже.
На рисунке показан пример вызова функции pool.map(), отображаемый вдоль строки кода, взятой из функции multiprocessing.pool.worker, где задача, считанная из inqueue распаковывается. worker является основным основным -function в MainThread пула-рабочего процесса. func -argument указано в бассейне -method будет соответствовать только func -variable внутри worker -function для методов одного вызова, как apply_async и для imap с chunksize=1. Для остальной части бассейна -method S с chunksize -parameter обработка -function func будет картостроитель -function (mapstar или starmapstar). Эта функция отображает пользовательский func -parameter на каждый элемент передаваемого фрагмента итерируемого (-> "map-tasks"). Время, которое требуется, определяет задачу также как единицу работы.
Taskel
В то время как использование слова "задача" для всей обработки одного блока соответствует коду в multiprocessing.pool, нет никаких указаний на то, как один вызов func, указанной пользователем, с одним элементом блока в качестве аргумента (ов).), следует упомянуть. Чтобы избежать путаницы, возникающей из-за конфликтов имен (подумайте о maxtasksperchild -parameter для пула __init__ -method), этот ответ будет относиться к отдельным единицам работы в рамках задачи как к Taskel.
Задача (из задачи + элемент) - это наименьшая единица работы в задаче. Это однократное выполнение функции, указанной в
func-parameterPool-method, вызываемой с аргументами, полученными из одного элемента переданного фрагмента. Задача состоит изchunksizeбольшого размера.
Распределение издержек (PO)
PO состоит из внутренних издержек Python и служебных данных для межпроцессного взаимодействия (IPC). Служебная нагрузка для каждой задачи в Python поставляется с кодом, необходимым для упаковки и распаковки задач и их результатов. Служебная нагрузка IPC сопровождается необходимой синхронизацией потоков и копированием данных между различными адресными пространствами (требуется два шага копирования: parent → queue → child). Количество накладных расходов IPC зависит от OS-, hardware- и размера данных, что затрудняет обобщение воздействия.
2. Цели распараллеливания
При использовании многопроцессорной обработки нашей общей целью (очевидно) является минимизация общего времени обработки для всех задач. Для достижения этой общей цели нашей технической задачей должна быть оптимизация использования аппаратных ресурсов.
Некоторые важные подцели для достижения технической цели:
- минимизировать издержки распараллеливания (наиболее известный, но не один: IPC)
- высокая загрузка всех процессорных ядер
- ограничение использования памяти для предотвращения чрезмерного подкачки ОС (очистки)
Сначала задачи должны быть достаточно сложными (интенсивными) в вычислительном отношении, чтобы вернуть ПО, которое мы должны заплатить за распараллеливание. Актуальность ПО уменьшается с увеличением абсолютного времени вычислений на одно задание. Или, другими словами, чем больше абсолютное время вычислений для каждой задачи, тем менее значимой становится потребность в сокращении ПО. Если ваши вычисления займут несколько часов на одну задачу, накладные расходы IPC будут незначительными по сравнению с ними. Основной задачей здесь является предотвращение простоя рабочих процессов после распределения всех задач. Держа все ядра загруженными, значит, мы распараллеливаемся как можно больше.
3. Сценарии распараллеливания
Какие факторы определяют оптимальный аргумент размера фрагмента для таких методов, как multiprocessing.Pool.map()
Основным фактором, о котором идет речь, является то, сколько времени вычислений может варьироваться в зависимости от наших задач. Чтобы назвать это, выбор оптимального размера кусочка определяется...
Коэффициент вариации (CV) для расчета времени на одно задание.
Два крайних сценария в масштабе, следующие из степени этого изменения:
- Для всех задач требуется одинаковое время вычислений.
- Задача может занять несколько секунд или дней, чтобы закончить.
Для лучшей запоминаемости я буду ссылаться на эти сценарии как:
- Плотный сценарий
- Широкий сценарий
Плотный сценарий
В плотном сценарии было бы желательно распределить все задачи одновременно, чтобы свести к минимуму необходимое IPC и переключение контекста. Это означает, что мы хотим создать только столько кусков, сколько рабочих процессов существует. Как уже указывалось выше, вес ПО увеличивается с более коротким временем вычислений на одно задание.
Для максимальной пропускной способности мы также хотим, чтобы все рабочие процессы были заняты до тех пор, пока не будут выполнены все задачи (без рабочих на холостом ходу). Для этой цели распределенные порции должны быть одинакового размера или близки к.
Широкий сценарий
Основным примером для широкого сценария будет проблема оптимизации, когда результаты либо быстро сходятся, либо вычисления могут занять часы, если не дни. Обычно невозможно предсказать, какую смесь "легких задач" и "тяжелых задач" будет содержать задание в таком случае, поэтому не рекомендуется распределять слишком много задач одновременно в пакете задач. Распределение меньшего количества задач одновременно, чем это возможно, означает увеличение гибкости планирования. Это необходимо для достижения нашей подцели высокой эффективности использования всех ядер.
Если методы Pool по умолчанию будут полностью оптимизированы для плотного сценария, они будут все больше создавать неоптимальные временные характеристики для каждой проблемы, расположенной ближе к широкому сценарию.
4. Риски Chunksize> 1
Рассмотрим пример упрощенного псевдокода широкого сценария -iterable, который мы хотим передать в пул -method:
good_luck_iterable = [60, 60, 86400, 60, 86400, 60, 60, 84600]
Вместо реальных значений мы притворяемся, что видим необходимое время вычисления в секундах, для простоты только 1 минуту или 1 день. Мы предполагаем, что в пуле четыре рабочих процесса (на четырех ядрах), а для chunksize задано значение 2. Поскольку порядок будет сохранен, куски, отправленные рабочим, будут такими:
[(60, 60), (86400, 60), (86400, 60), (60, 84600)]
Поскольку у нас достаточно рабочих и время вычислений достаточно велико, мы можем сказать, что каждый рабочий процесс получит кусок, над которым он будет работать в первую очередь. (Это не должно иметь место для быстрого выполнения задач). Далее мы можем сказать, что вся обработка займет около 86400 + 60 секунд, потому что это наибольшее общее время вычислений для порции в этом искусственном сценарии, и мы распределяем порции только один раз.
Теперь рассмотрим эту итерацию, в которой только один элемент меняет свою позицию по сравнению с предыдущей итерацией:
bad_luck_iterable = [60, 60, 86400, 86400, 60, 60, 60, 84600]
... и соответствующие куски:
[(60, 60), (86400, 86400), (60, 60), (60, 84600)]
Просто неудача с сортировкой нашей итерации почти вдвое (86400 + 86400) нашего общего времени обработки! Рабочий, получающий порочный (86400, 86400) -chunk, блокирует вторую тяжелую задачу в своей задаче, чтобы распределить его одному из рабочих на холостом ходу, уже покончившим с (60, 60) -chunk. Мы, очевидно, не рискнули бы таким неприятным исходом, если бы мы установили chunksize=1.
Это риск больших кусков. С более высокими размерами блоков мы торгуем гибкостью планирования за меньшие накладные расходы, а в случаях, подобных описанным выше, это плохая сделка.
Как мы увидим в главе 6. Количественная оценка эффективности алгоритма, большие размеры фрагментов также могут привести к неоптимальным результатам для плотных сценариев.
5. Пул Chunksize-Алгоритм
Ниже вы найдете слегка измененную версию алгоритма внутри исходного кода. Как видите, я обрезал нижнюю часть и обернул ее в функцию для внешнего вычисления аргумента chunksize. Я также заменил 4 на factor и передал вызовы len().
# mp_utils.py
def calc_chunksize(n_workers, len_iterable, factor=4):
"""Calculate chunksize argument for Pool-methods.
Resembles source-code within 'multiprocessing.pool.Pool._map_async'.
"""
chunksize, extra = divmod(len_iterable, n_workers * factor)
if extra:
chunksize += 1
return chunksize
Чтобы убедиться, что мы все на одной странице, вот что делает divmod:
divmod(x, y) - встроенная функция, которая возвращает (x//y, x%y). x//y - это деление по полу, которое возвращает округленное вниз число от x/y, а x % y - это операция по модулю, возвращающая остаток от x/y. Следовательно, например, divmod(10, 3) возвращает (3, 1).
Теперь, когда вы посмотрите на chunksize, extra = divmod(len_iterable, n_workers * 4), вы заметите, что n_workers - это делитель y по x/y и умножение на 4, без дальнейшей корректировки, if extra: chunksize +=1, приводит к начальному размеру фрагмента по крайней мере в четыре раза меньше (для len_iterable >= n_workers * 4), чем это было бы в противном случае.
Для просмотра эффекта умножения на 4 на промежуточный результат размера фрагмента рассмотрим следующую функцию:
def compare_chunksizes(len_iterable, n_workers=4):
"""Calculate naive chunksize, Pool stage-1 chunksize and the chunksize
for Pool complete algorithm. Return chunksizes and the real factors by
which naive chunksizes are bigger.
"""
cs_naive = len_iterable // n_workers or 1 # naive approach
cs_pool1 = len_iterable // (n_workers * 4) or 1 # incomplete pool algo.
cs_pool2 = calc_chunksize(n_workers, len_iterable)
real_factor_pool1 = cs_naive / cs_pool1
real_factor_pool2 = cs_naive / cs_pool2
return cs_naive, cs_pool1, cs_pool2, real_factor_pool1, real_factor_pool2
Вышеуказанная функция вычисляет наивный размер фрагмента (cs_naive) и размер cs_naive первого шага алгоритма размера фрагмента пула (cs_pool1), а также размер фрагмента для полного алгоритма cs_pool2 (cs_pool2). Далее он вычисляет реальные коэффициенты rf_pool1 = cs_naive/cs_pool1 и rf_pool2 = cs_naive/cs_pool2, которые говорят нам, во сколько раз наивно рассчитанные размеры фрагментов больше, чем внутренние версии пула.
Ниже вы видите две фигуры, созданные с помощью этой функции. Левый рисунок просто показывает размеры фрагментов для n_workers=4 вплоть до итерированной длины до 500. На правом рисунке показаны значения для rf_pool1. Для итерируемой длины 16 реальный фактор становится >=4 (для len_iterable >= n_workers * 4), и его максимальное значение равно 7 для итерируемой длины 28-31. Это значительное отклонение от исходного фактора 4, к которому сходится алгоритм для более длинных итераций. "Более длинный" здесь относительный и зависит от количества указанных работников.
Помните, что в chunksize cs_pool1 прежнему отсутствует extra -adjustment с остатком от divmod содержащимся в cs_pool2 из полного алгоритма.
Алгоритм продолжается с:
if extra:
chunksize += 1
Теперь в случаях, когда есть остаток (extra от divmod-операции), увеличение размера фрагмента на 1, очевидно, не может сработать для каждой задачи. В конце концов, если бы это было так, не было бы остатка для начала.
Как вы можете видеть на рисунках ниже, " дополнительная обработка " приводит к тому, что реальный коэффициент для rf_pool2 теперь сходится к 4 ниже 4 а отклонение несколько плавнее. Стандартное отклонение для n_workers=4 и len_iterable=500 падает с 0.5233 для rf_pool1 до 0.4115 для rf_pool2.
В конце концов, увеличение chunksize на 1 приводит к тому, что последняя переданная задача имеет размер len_iterable % chunksize or chunksize.
Однако чем интереснее и как мы увидим позже, тем больше эффект дополнительной обработки можно наблюдать для числа сгенерированных кусков (n_chunks). Для достаточно длинных итераций алгоритм завершения пула chunksize (n_pool2 на рисунке ниже) стабилизирует количество фрагментов при n_chunks == n_workers * 4. Напротив, наивный алгоритм (после первоначальной отрыжки) продолжает чередоваться между n_chunks == n_workers и n_chunks == n_workers + 1 мере увеличения длины итерируемого.
Ниже вы найдете две улучшенные данные -function для пула и простой алгоритм chunksize. Вывод этих функций будет необходим в следующей главе.
# mp_utils.py
from collections import namedtuple
Chunkinfo = namedtuple(
'Chunkinfo', ['n_workers', 'len_iterable', 'n_chunks',
'chunksize', 'last_chunk']
)
def calc_chunksize_info(n_workers, len_iterable, factor=4):
"""Calculate chunksize numbers."""
chunksize, extra = divmod(len_iterable, n_workers * factor)
if extra:
chunksize += 1
# '+ (len_iterable % chunksize > 0)' exploits that 'True == 1'
n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
# exploit '0 == False'
last_chunk = len_iterable % chunksize or chunksize
return Chunkinfo(
n_workers, len_iterable, n_chunks, chunksize, last_chunk
)
Не смущайтесь, возможно, неожиданным взглядом calc_naive_chunksize_info. extra от divmod не используется для вычисления размера фрагмента.
def calc_naive_chunksize_info(n_workers, len_iterable):
"""Calculate naive chunksize numbers."""
chunksize, extra = divmod(len_iterable, n_workers)
if chunksize == 0:
chunksize = 1
n_chunks = extra
last_chunk = chunksize
else:
n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
last_chunk = len_iterable % chunksize or chunksize
return Chunkinfo(
n_workers, len_iterable, n_chunks, chunksize, last_chunk
)
6. Количественная оценка эффективности алгоритма
Теперь, после того, как мы увидели, как выходные данные алгоритма chunksize Pool выглядят иначе, чем выходные данные наивного алгоритма...
- Как определить, действительно ли подход к пулу улучшает что-либо?
- И что именно это может быть?
Как показано в предыдущей главе, для более длинных итераций (большее число задач) алгоритм пула chunksize-алгоритм приблизительно делит итерируемое на четыре раза больше фрагментов, чем наивный метод. Меньшие куски означают больше задач, а больше задач - больше издержек распараллеливания (PO), затраты, которые должны быть сопоставлены с преимуществом повышенной гибкости планирования (вспомните "Риски Chunksize> 1").
По довольно очевидным причинам базовый алгоритм chunksize пула не может сравниться с нами в гибкости планирования и PO. Служебные расходы IPC зависят от OS-, hardware- и размера данных. Алгоритм не может знать, на каком оборудовании мы запускаем наш код, и не имеет понятия, сколько времени займет выполнение задачи. Это эвристика, обеспечивающая базовую функциональность для всех возможных сценариев. Это означает, что он не может быть оптимизирован для какого-либо конкретного сценария. Как упоминалось ранее, ПО также становится все менее важной для увеличения времени вычислений на одно задание (отрицательная корреляция).
Когда вы вспоминаете Цели распараллеливания из главы 2, одним из пунктов было следующее:
- высокая загрузка всех процессорных ядер
Вышеупомянутый алгоритм пула chunksize-алгоритма, который можно попытаться улучшить, - это минимизация простоя рабочих процессов и, соответственно, использование процессорных ядер.
Повторяющийся вопрос о SO в отношении multiprocessing.Pool. Люди задаются вопросом о неиспользуемых ядрах/неработающих рабочих процессах в ситуациях, когда можно ожидать, что все рабочие процессы заняты. Хотя на это может быть много причин, простаивающие рабочие процессы ближе к концу вычислений - это наблюдение, которое мы часто можем сделать, даже с плотными сценариями (равное время вычислений на одно задание) в тех случаях, когда число работников не является делителем числа. кусков (n_chunks % n_workers > 0).
Вопрос сейчас:
Как мы можем практически перевести наше понимание размеров кусков во что-то, что позволяет нам объяснить наблюдаемое использование работника, или даже сравнить эффективность различных алгоритмов в этом отношении?
6.1 Модели
Для получения более глубокого понимания здесь нам нужна форма абстракции параллельных вычислений, которая упрощает чрезмерно сложную реальность до управляемой степени сложности, сохраняя при этом значение в определенных границах. Такая абстракция называется моделью. Реализация такой " модели распараллеливания" (PM) генерирует метаданные (временные метки), отображаемые рабочим, как реальные вычисления, если бы данные собирались. Сгенерированные моделью метаданные позволяют прогнозировать метрики параллельных вычислений при определенных ограничениях.
Одной из двух подмоделей в определенном здесь PM является модель распределения (DM). DM объясняет, как атомные единицы работы (Taskels) распределяются по параллельным рабочим и времени, когда нет других факторов, кроме соответствующего алгоритма chunksize, количества рабочих, входных данных -iterable (количество Taskels) и их длительности вычислений считается. Это означает, что любая форма накладных расходов не включена.
Для получения полного PM DM расширяется с помощью модели служебных данных (OM), представляющей различные формы служебных данных параллелизации (PO). Такая модель должна быть откалибрована для каждого узла отдельно (зависимости hardware-, OS-). Сколько форм служебных данных представлено в ОМ, остается открытым, и поэтому могут существовать несколько ОМ с различной степенью сложности. Какой уровень точности необходим для реализации OM, определяется общим весом PO для конкретного вычисления. Более короткие задачи приводят к большему весу ПО, что, в свою очередь, требует более точного ОМ, если мы пытались предсказать эффективность распараллеливания (PE).
6.2 Параллельное расписание (PS)
Параллельное расписание - это двумерное представление параллельных вычислений, где ось X представляет время, а ось Y представляет пул параллельных рабочих. Количество рабочих и общее время вычислений отмечают протяженность прямоугольника, в котором нарисованы меньшие прямоугольники. Эти меньшие прямоугольники представляют атомные единицы работы (задачи).
Ниже вы найдете визуализацию PS, построенную с данными из алгоритма DM chunksize для пула для плотного сценария.
- Ось X разделена на равные единицы времени, где каждая единица соответствует времени вычисления, которое требуется для задачи.
- Ось Y делится на количество рабочих процессов, которые использует пул.
- Задача здесь отображается как наименьший прямоугольник голубого цвета, помещенный во временную шкалу (график) анонимного рабочего процесса.
- Задача - это одна или несколько задач на рабочем графике, которые постоянно выделяются одним и тем же оттенком.
- Единицы времени холостого хода представлены красным цветом.
- Параллельное расписание разбито на разделы. Последний раздел является хвостовой частью.
Названия составных частей можно увидеть на картинке ниже.
В полном PM, включая OM, доля холостого хода не ограничивается хвостом, но также включает пространство между задачами и даже между задачами.
6.3 Эффективность
Замечания:
Начиная с более ранних версий этого ответа, "Эффективность распараллеливания (PE)" была переименована в "Эффективность распределения (DE)". PE теперь относится к накладным расходам, включая эффективность.
Представленные выше модели позволяют количественно оценить коэффициент использования работника. Мы можем различить:
- Эффективность распределения (DE) - рассчитывается с помощью DM (или упрощенного метода для плотного сценария).
- Эффективность распараллеливания (PE) - либо рассчитывается с помощью калиброванного PM (прогноз), либо рассчитывается на основе метаданных реальных вычислений.
Важно отметить, что вычисленные коэффициенты полезного действия не коррелируют автоматически с более быстрым общим вычислением для данной проблемы распараллеливания. Использование работника в этом контексте различает только работника, у которого есть начальная, но незаконченная задача, и работника, у которого нет такой "открытой" задачи. Это означает, что возможный холостой ход в течение промежутка времени не регистрируется.
Все вышеупомянутые эффективности в основном получаются путем вычисления коэффициента деления Busy Share/Parallel Schedule. Разница между DE и PE заключается в том, что Busy Share занимает меньшую часть общего параллельного расписания для расширенного PM.
Далее в этом ответе будет обсуждаться только простой метод расчета DE для плотного сценария. Этого достаточно для сравнения различных алгоритмов chunksize, так как...
- ... DM - это часть PM, которая меняется в зависимости от используемых алгоритмов chunksize.
- ... Плотный сценарий с равной продолжительностью вычислений на одно задание отображает "стабильное состояние", для которого эти промежутки времени выпадают из уравнения. Любой другой сценарий может привести к случайным результатам, так как порядок задач будет иметь значение.
6.3.1 Абсолютная эффективность распределения (ADE)
Эту базовую эффективность можно рассчитать в целом, разделив занятую долю на весь потенциал параллельного расписания:
Абсолютная эффективность распределения (ADE)= занятая доля/параллельное расписание
Для плотного сценария упрощенный код расчета выглядит следующим образом:
# mp_utils.py
def calc_ade(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
"""Calculate Absolute Distribution Efficiency (ADE).
'len_iterable' is not used, but contained to keep a consistent signature
with 'calc_rde'.
"""
if n_workers == 1:
return 1
potential = (
((n_chunks // n_workers + (n_chunks % n_workers > 1)) * chunksize)
+ (n_chunks % n_workers == 1) * last_chunk
) * n_workers
n_full_chunks = n_chunks - (chunksize > last_chunk)
taskels_in_regular_chunks = n_full_chunks * chunksize
real = taskels_in_regular_chunks + (chunksize > last_chunk) * last_chunk
ade = real / potential
return ade
Если доля холостого хода отсутствует, доля занятого будет равна параллельному расписанию, следовательно, мы получим ADE в размере 100%. В нашей упрощенной модели это сценарий, в котором все доступные процессы будут заняты все время, необходимое для обработки всех задач. Другими словами, вся работа эффективно распределяется до 100 процентов.
Но почему я продолжаю называть PE абсолютным PE здесь?
Чтобы понять это, мы должны рассмотреть возможный случай для размера фрагмента (cs), который обеспечивает максимальную гибкость планирования (также, число Горцев может быть. Совпадение?):
___________________________________ ~ ONE ~ ___________________________________
Если, например, у нас есть четыре рабочих процесса и 37 задач, рабочие будут работать на холостом ходу даже с chunksize=1 только потому, что n_workers=4 не является делителем 37. Остальная часть деления n_workers=4 равна 1. Этот единственный Оставшаяся часть работы должна быть обработана единственным работником, а остальные три - на холостом ходу.
Кроме того, еще будет один рабочий на холостом ходу с 39 задачами, как вы можете видеть на рисунке ниже.
Когда вы сравните верхнее параллельное расписание для chunksize=1 с приведенной ниже версией для chunksize=3, вы заметите, что верхнее параллельное расписание меньше, а временная шкала на оси x короче. Теперь должно стать очевидным, как неожиданно большие куски также могут привести к увеличению общего времени вычислений даже для плотных сценариев.
Но почему бы просто не использовать длину оси X для расчетов эффективности?
Потому что накладные расходы не содержатся в этой модели. Это будет отличаться для обоих кусков, следовательно, ось X не является прямо сопоставимой. Затраты по-прежнему могут привести к увеличению общего времени вычислений, как показано в случае 2 на рисунке ниже.
6.3.2 Относительная эффективность распределения (RDE)
Значение ADE не содержит информацию о том, возможно ли лучшее распределение задач с размером фрагмента, равным 1. Лучшее значение здесь по-прежнему означает меньшую долю холостого хода.
Чтобы получить значение DE, скорректированное на максимально возможное значение DE, мы должны разделить рассмотренную ADE на ADE, chunksize=1 для chunksize=1.
Относительная эффективность распределения (RDE)= ADE_cs_x/ADE_cs_1
Вот как это выглядит в коде:
# mp_utils.py
def calc_rde(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
"""Calculate Relative Distribution Efficiency (RDE)."""
ade_cs1 = calc_ade(
n_workers, len_iterable, n_chunks=len_iterable,
chunksize=1, last_chunk=1
)
ade = calc_ade(n_workers, len_iterable, n_chunks, chunksize, last_chunk)
rde = ade / ade_cs1
return rde
RDE, как определено здесь, по сути является рассказом о хвосте параллельного расписания. На RDE влияет максимально эффективный размер кусочка, содержащийся в хвосте. (Этот хвост может иметь длину chunksize или last_chunk оси chunksize.) Это приводит к тому, что RDE естественным образом сходится к 100% (даже) для всех видов "хвостов", как показано на рисунке ниже.
Низкий RDE...
- является сильным намеком на оптимизацию потенциала.
- естественно, становится менее вероятным для более длинных итераций, потому что относительная хвостовая часть общего параллельного расписания сокращается.
найти часть II этого ответа здесь ниже.