Пример факториального алгоритма времени O (n!)

Я изучаю временную сложность в школе, и наш основной фокус, по-видимому, заключается в алгоритмах полиномиального времени 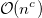<code>O(n^c)</code> и алгоритмах квазилинейного времени 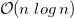<code>O(nlog(n))</code> со случайным алгоритмом экспоненциального времени 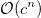<code>O(c^n)</code> в качестве примера времени выполнения перспектива. Тем не менее, проблема с более сложными сложностями никогда не охватывалась.

Я хотел бы увидеть пример проблемы с алгоритмическим решением, которое выполняется в факториальное время 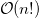<code>O(n!)</code>. Алгоритм может быть наивным подходом к решению проблемы, но не может быть искусственно раздутым, чтобы работать в факториальное время.

Extra street-cred, если алгоритм факториального времени является наиболее известным алгоритмом для решения проблемы.

Ответы

Ответ 1

Сгенерировать все перестановки списка

У вас есть списки n!, поэтому вы не можете добиться большей эффективности, чем O(n!).

Ответ 2

Traveling Salesman имеет наивное решение, которое O (n!), но имеет динамическое программирующее решение, что O (n ^ 2 * 2 ^ п)

Ответ 3

Список всех перестановок массива - O (n!). Ниже приведена рекурсивная реализация с использованием метода подкачки. Рекурсия находится внутри цикла for, и элементы в массиве меняются местами, пока не останется больше элементов. Как видно из результата, количество элементов в массиве равно n!. Каждая перестановка - это операция, и есть n! операции.

def permutation(array, start, result)
    if (start == array.length) then
        result << array.dup  
    end
    for i in start..array.length-1 do
        array[start], array[i] = array[i], array[start]
        permutation(array, start+1,result)
        array[start], array[i] = array[i], array[start]
    end 
    result   
end        


p permutation([1,2,3], 0, []).count  #> 6 = 3!
p permutation([1,2,3,4], 0, []).count #> 24 = 4!
p permutation([1,2,3,4,5], 0, []).count #> 120 = 5!