Ответ 1
Вы можете использовать метод экспоненциальной матрицы (метод линейной рекурсии). Подробное описание и процедуру можно найти в этом блоге. Время выполнения - O (log n).
Я не думаю, что есть лучший способ сделать это.
Мне было интересно, как можно найти n-й член последовательности фибоначчи для очень большого значения n, скажем, 1000000. Используя уравнение регрессии школьной школы fib(n)=fib(n-1)+fib(n-2), требуется найти 50-й срок!
После googling я узнал о формуле Бине, но это не подходит для значений n > 79, как сказано здесь
Есть ли алгоритм для этого, как и для нахождения простых чисел?
Вы можете использовать метод экспоненциальной матрицы (метод линейной рекурсии). Подробное описание и процедуру можно найти в этом блоге. Время выполнения - O (log n).
Я не думаю, что есть лучший способ сделать это.
Вы можете сэкономить много времени, используя memoization. Например, сравните следующие две версии (в JavaScript):
Версия 1: обычная рекурсия
var fib = function(n) {
return n < 2 ? n : fib(n - 1) + fib(n - 2);
};
Версия 2: memoization
а. используйте underscore библиотека
var fib2 = _.memoize(function(n) {
return n < 2 ? n : fib2(n - 1) + fib2(n - 2);
});
В. библиотека-бесплатно
var fib3 = (function(){
var memo = {};
return function(n) {
if (memo[n]) {return memo[n];}
return memo[n] = (n <= 2) ? 1 : fib3(n-2) + fib3(n-1);
};
})();
Первая версия занимает более 3 минут для n = 50 (в Chrome), а вторая занимает меньше 5 мс! Вы можете проверить это в jsFiddle.
Не удивительно, если мы знаем, что временная сложность версии 1 экспоненциальна (O (2 N/2)), а версия 2 линейна (O (N)).
Версия 3: матричное умножение
Кроме того, мы можем даже сократить временную сложность до O (log (N)), вычислив умножение N-матриц.
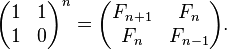
где F n обозначает n-й член последовательности Фибоначчи.
Используйте идентификаторы повторения http://en.wikipedia.org/wiki/Fibonacci_number#Other_identities, чтобы найти n -th number в шагах log(n). Для этого вам придется использовать произвольные целые числа точности. Или вы можете рассчитать точный ответ по модулю некоторого фактора, используя модульную арифметику на каждом шаге.



Заметив, что 3n+3 == 3(n+1), мы можем разработать однорекурсивную функцию, которая вычисляет два последовательных числа Фибоначчи на каждом шаге, деля на n на 3 и выбирая соответствующую формулу в соответствии с остаточным значением, IOW он вычисляет пару @(3n+r,3n+r+1), r=0,1,2 из пары @(n,n+1) за один шаг, поэтому нет двойной рекурсии, и никакая memoization не требуется.
Код Haskell здесь.
F(2n-1) = F(n-1)^2 + F(n)^2 === a' = a^2 + b^2
F(2n) = 2 F(n-1) F(n) + F(n)^2 === b' = 2ab + b^2
похоже, приводит к более быстрому коду. Использование "Тождества последовательности Lucas" может быть самым быстрым (это обязано пользователю: primo, который ссылается на эту реализацию).
Я согласен с ответом Уэйна Руни, что оптимальное решение будет выполнено за O (log n) шагов, однако общая сложность во время выполнения будет зависеть от сложности используемого алгоритма умножения. Например, при использовании умножения Карацубы общая сложность во время выполнения будет O (n log 2 3) ≈ O (n 1,585). 1
Тем не менее, возведение в матрицу не обязательно является лучшим способом для этого. Как заметил разработчик Project Nayuki, возведение в степень матрицы влечет за собой избыточные вычисления, которые можно удалить. От автора описание:
Учитывая F k и F k + 1, мы можем вычислить это:
Обратите внимание, что для этого требуется только 3 умножения BigInt-BigInt на разделение, а не 8, как для возведения в матрицу.
Мы все еще можем сделать немного лучше, чем это, хотя. Одна из самых элегантных личностей Фибоначчи связана с числами Лукаса:
где L n - это n- йномер Лукаса. Эта идентичность может быть далее обобщена как:
Существует несколько более или менее эквивалентных способов рекурсивного продолжения, но наиболее логичным представляется использование F n и L n. Дополнительные идентификаторы, используемые в приведенной ниже реализации, могут быть найдены или получены из идентификаторов, перечисленных для последовательностей Лукаса:
Выполнение этого способа требует только двух умножений BigInt-BigInt на одно деление и только одного для окончательного результата. Это примерно на 20% быстрее, чем код, предоставленный Project Nayuki (тестовый скрипт). Примечание: исходный источник был немного изменен (улучшен), чтобы обеспечить справедливое сравнение.
def fibonacci(n):
def fib_inner(n):
'''Returns F[n] and L[n]'''
if n == 0:
return 0, 2
u, v = fib_inner(n >> 1)
q = (n & 2) - 1
u, v = u * v, v * v + 2*q
if (n & 1):
u1 = (u + v) >> 1
return u1, 2*u + u1
return u, v
u, v = fib_inner(n >> 1)
if (n & 1):
q = (n & 2) - 1
u1 = (u + v) >> 1
return v * u1 + q
return u * v
Серый Бород указывает, что вышеупомянутый результат уже был улучшен Такахаси (2000) 2 отметив, что возведение в квадрат BigInt обычно (и особенно для алгоритма Шёнхаге-Штрассена) менее затратно в вычислительном отношении, чем умножение BigInt. Автор предлагает итерацию, разделяющую на F n и L n, используя следующие тождества:
Итерация таким образом потребует двух квадратов BigInt на разделение, а не квадрата BigInt и умножения BigInt, как указано выше. Как и ожидалось, время выполнения измеримо быстрее, чем приведенная выше реализация для очень больших n, но несколько медленнее для малых значений (n <25000).
Тем не менее, это может быть немного улучшено. Автор утверждает, что "известно, что алгоритм Произведения чисел Лукаса использует наименьшее количество битовых операций для вычисления числа Фибоначчи F n ". Затем автор решает адаптировать алгоритм Произведения чисел Лукаса, который в то время был самым быстрым из известных, с разбивкой по F n и L n. Заметим, однако, что L n всегда используется только для вычисления F n + 1. Это кажется несколько расточительным, если учесть следующие особенности:
где первое взято непосредственно у Такахаси, второе - результат метода возведения в степень матрицы (также отмеченный Наюки), а третье - результат сложения двух предыдущих. Это позволяет очевидное разбиение на F n и F n + 1. В результате требуется одно меньшее добавление BigInt и, что важно, еще одно деление на 2 для четного n; для нечетного n выгода увеличивается вдвое. На практике это значительно быстрее, чем метод, предложенный Такахаши для малых n (на 10-15% быстрее), и незначительно быстрее для очень больших n (тестовый сценарий).
def fibonacci(n):
def fib_inner(n):
'''Returns F[n] and F[n+1]'''
if n == 0:
return 0, 1
u, v = fib_inner(n >> 1)
q = (n & 2) - 1
u *= u
v *= v
if (n & 1):
return u + v, 3*v - 2*(u - q)
return 2*(v + q) - 3*u, u + v
u, v = fib_inner(n >> 1)
# L[m]
l = 2*v - u
if (n & 1):
q = (n & 2) - 1
return v * l + q
return u * l
1 Видно, что количество цифр (или битов) F n ~ O (n) как:
Сложность времени выполнения с использованием умножения Карацубы может быть рассчитана следующим образом:
2 Такахаши, Д. (2000), "Быстрый алгоритм вычисления больших чисел Фибоначчи" (PDF), Письма обработки информации 75, с. 243–246.
Большинство людей уже дали вам ссылку, объясняющую нахождение N-го числа Фибоначчи, кстати, алгоритм Power работает так же с незначительными изменениями.
В любом случае это мое решение O (log N).
package algFibonacci;
import java.math.BigInteger;
public class algFibonacci {
// author Orel Eraki
// Fibonacci algorithm
// O(log2 n)
public static BigInteger Fibonacci(int n) {
int num = Math.abs(n);
if (num == 0) {
return BigInteger.ZERO;
}
else if (num <= 2) {
return BigInteger.ONE;
}
BigInteger[][] number = { { BigInteger.ONE, BigInteger.ONE }, { BigInteger.ONE, BigInteger.ZERO } };
BigInteger[][] result = { { BigInteger.ONE, BigInteger.ONE }, { BigInteger.ONE, BigInteger.ZERO } };
while (num > 0) {
if (num%2 == 1) result = MultiplyMatrix(result, number);
number = MultiplyMatrix(number, number);
num/= 2;
}
return result[1][1].multiply(BigInteger.valueOf(((n < 0) ? -1:1)));
}
public static BigInteger[][] MultiplyMatrix(BigInteger[][] mat1, BigInteger[][] mat2) {
return new BigInteger[][] {
{
mat1[0][0].multiply(mat2[0][0]).add(mat1[0][1].multiply(mat2[1][0])),
mat1[0][0].multiply(mat2[0][1]).add(mat1[0][1].multiply(mat2[1][1]))
},
{
mat1[1][0].multiply(mat2[0][0]).add(mat1[1][1].multiply(mat2[1][0])),
mat1[1][0].multiply(mat2[0][1]).add(mat1[1][1].multiply(mat2[1][1]))
}
};
}
public static void main(String[] args) {
System.out.println(Fibonacci(8181));
}
}
Для вычисления чисел Фибоначчи рекурсивный алгоритм является одним из худших способов. Простое добавление двух предыдущих чисел в цикл for (называемый итерационным методом) не займет 2-3 минуты, чтобы вычислить 50-й элемент.
Для вычисления произвольно больших элементов последовательности Фибоначчи вам нужно будет использовать формулу с замкнутой формой - формулу Бине и использовать математику с произвольной точностью, чтобы обеспечить достаточную точность вычисления ответа.
Однако при использовании отношения повторения не требуется 2-3 минуты, чтобы рассчитать 50-й срок - вы должны иметь возможность вычислять сроки в миллиарды в течение нескольких секунд на любой современной машине. Похоже, вы используете полностью рекурсивную формулу, что приводит к комбинаторному взрыву рекурсивных вычислений. Простая итеративная формула намного быстрее.
В частности: рекурсивное решение:
int fib(int n) {
if (n < 2)
return 1;
return fib(n-1) + fib(n-2)
}
... и откиньтесь назад и наблюдайте переполнение стека.
Итеративное решение:
int fib(int n) {
if (n < 2)
return 1;
int n_1 = 1, n_2 = 1;
for (int i = 2; i <= n; i += 1) {
int n_new = n_1 + n_2;
n_1 = n_2;
n_2 = n_new;
}
return n_2;
}
Обратите внимание, как мы по существу вычисляем следующий член n_new из предыдущих терминов n_1 и n_2, затем "перетасовка" всех членов вниз для следующей итерации. При длительности работы, линейной по значению n, это займет несколько секунд для n в миллиардах (после переполнения целых чисел для ваших промежуточных переменных) на современной машине гигагерца.
Во-первых, вы можете сформировать идею самого высокого термина из самого большого известного термина Фибоначчи. также см. пошаговое представление рекурсивного представления функции Фибоначчи. Интересный подход к этой теме в этой статье. Кроме того, попробуйте прочитать об этом в худшем алгоритме в мире? ,
У меня есть исходный код в c для вычисления даже 3500-го числа фибоначчи: - для более подробной информации посетите
http://codingloverlavi.blogspot.in/2013/04/fibonacci-series.html
исходный код в C: -
#include<stdio.h>
#include<conio.h>
#define max 2000
int arr1[max],arr2[max],arr3[max];
void fun(void);
int main()
{
int num,i,j,tag=0;
clrscr();
for(i=0;i<max;i++)
arr1[i]=arr2[i]=arr3[i]=0;
arr2[max-1]=1;
printf("ENTER THE TERM : ");
scanf("%d",&num);
for(i=0;i<num;i++)
{
fun();
if(i==num-3)
break;
for(j=0;j<max;j++)
arr1[j]=arr2[j];
for(j=0;j<max;j++)
arr2[j]=arr3[j];
}
for(i=0;i<max;i++)
{
if(tag||arr3[i])
{
tag=1;
printf("%d",arr3[i]);
}
}
getch();
return 1;
}
void fun(void)
{
int i,temp;
for(i=0;i<max;i++)
arr3[i]=arr1[i]+arr2[i];
for(i=max-1;i>0;i--)
{
if(arr3[i]>9)
{
temp=arr3[i];
arr3[i]%=10;
arr3[i-1]+=(temp/10);
}
}
}
Я решил проблемы с UVA: 495 - Fibonacci Freeze
Он генерирует все числа Фибоначчи до 5000 и выводит выходные данные для заданных входов (диапазон 1-5000).
Принимается с временем выполнения 00.00 сек.
Число Фибоначчи для 5000:
3878968454388325633701916308325905312082127714646245106160597214895550139044037097010822916462210669479293452858882973813483102008954982940361430156911478938364216563944106910214505634133706558656238254656700712525929903854933813928836378347518908762970712033337052923107693008518093849801803847813996748881765554653788291644268912980384613778969021502293082475666346224923071883324803280375039130352903304505842701147635242270210934637699104006714174883298422891491273104054328753298044273676822977244987749874555691907703880637046832794811358973739993110106219308149018570815397854379195305617510761053075688783766033667355445258844886241619210553457493675897849027988234351023599844663934853256411952221859563060475364645470760330902420806382584929156452876291575759142343809142302917491088984155209854432486594079793571316841692868039545309545388698114665082066862897420639323438488465240988742395873801976993820317174208932265468879364002630797780058759129671389634214252579116872755600360311370547754724604639987588046985178408674382863125
#include<stdio.h>
#include<string.h>
#define LIMIT 5001
#define MAX 1050
char num[LIMIT][MAX];
char result[MAX];
char temp[MAX];
char* sum(char str1[], char str2[])
{
int len1 = strlen(str1);
int len2 = strlen(str2);
int minLen, maxLen;
int i, j, k;
if (len1 > len2)
minLen = len2, maxLen = len1;
else
minLen = len1, maxLen = len2;
int carry = 0;
for (k = 0, i = len1 - 1, j = len2 - 1; k<minLen; k++, i--, j--)
{
int val = (str1[i] - '0') + (str2[j] - '0') + carry;
result[k] = (val % 10) + '0';
carry = val / 10;
}
while (k < len1)
{
int val = str1[i] - '0' + carry;
result[k] = (val % 10) + '0';
carry = val / 10;
k++; i--;
}
while (k < len2)
{
int val = str2[j] - '0' + carry;
result[k] = (val % 10) + '0';
carry = val / 10;
k++; j--;
}
if (carry > 0)
{
result[maxLen] = carry + '0';
maxLen++;
result[maxLen] = '\0';
}
else
{
result[maxLen] = '\0';
}
i = 0;
while (result[--maxLen])
{
temp[i++] = result[maxLen];
}
temp[i] = '\0';
return temp;
}
void generateFibonacci()
{
int i;
num[0][0] = '0'; num[0][1] = '\0';
num[1][0] = '1'; num[1][1] = '\0';
for (i = 2; i <= LIMIT; i++)
{
strcpy(num[i], sum(num[i - 1], num[i - 2]));
}
}
int main()
{
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int N;
generateFibonacci();
while (scanf("%d", &N) == 1)
{
printf("The Fibonacci number for %d is %s\n", N, num[N]);
}
return 0;
}
Здесь версия python для вычисления n-го числа Фибоначчи в O (log (n))
def fib(n):
if n == 0:
return 0
if n == 1:
return 1
def matmul(M1, M2):
a11 = M1[0][0]*M2[0][0] + M1[0][1]*M2[1][0]
a12 = M1[0][0]*M2[0][1] + M1[0][1]*M2[1][1]
a21 = M1[1][0]*M2[0][0] + M1[1][1]*M2[1][0]
a22 = M1[1][0]*M2[0][1] + M1[1][1]*M2[1][1]
return [[a11, a12], [a21, a22]]
def matPower(mat, p):
if p == 1:
return mat
m2 = matPower(mat, p//2)
if p % 2 == 0:
return matmul(m2, m2)
else:
return matmul(matmul(m2, m2),mat)
Q = [[1,1],[1,0]]
q_final = matPower(Q, n-1)
return q_final[0][0]
Я написал реализацию C, которая поддерживает любую шкалу входного числа с GNU gmp.
Время для вычисления fib для одного числа - O(n), а пространство для кеша - O(1) (на самом деле он вычислял все fib для 0 ~ n).
fib_cached_gmp.c:
// fibonacci - cached algorithm - any scale of input with GMP,
#include <gmp.h>
#include <stdio.h>
#include <stdlib.h>
// a single step,
void fib_gmp_next(mpz_t *cache) {
mpz_add(cache[2], cache[0], cache[1]);
mpz_set(cache[0], cache[1]);
mpz_set(cache[1], cache[2]);
}
// figure fib for a single number, in O(n),
mpz_t *fib_gmp(int n, mpz_t *result) {
// init cache,
mpz_t cache[3]; // number: [fib(n-2), fib(n-1), fib(n)],
mpz_init(cache[0]);
mpz_init(cache[1]);
mpz_init(cache[2]);
mpz_set_si(cache[0], 0);
mpz_set_si(cache[1], 1);
while (n >= 2) {
fib_gmp_next(cache);
n--;
}
mpz_set(*result, cache[n]);
return result;
}
// test - print fib from 0 to n, tip: cache won't be reused betwwen any 2 input numbers,
void test_seq(int n) {
mpz_t result;
mpz_init(result);
for (int i = 0; i <= n; i++) {
gmp_printf("fib(%2d): %Zd\n", i, fib_gmp(i, &result));
}
}
// test - print fib for a single num,
void test_single(int x) {
mpz_t result;
mpz_init(result);
gmp_printf("fib(%d): %Zd\n", x, fib_gmp(x, &result));
}
int main() {
// test sequence,
test_seq(100);
// test single,
test_single(12345);
return 0;
}
Сначала установите gmp:
// for Ubuntu,
sudo apt-get install libgmp3-dev
Обобщение:
gcc fib_cached_gmp.c -lgmp
Выполнение:
./a.out
Пример вывода:
fib( 0): 0
fib( 1): 1
fib( 2): 1
fib( 3): 2
fib( 4): 3
fib( 5): 5
fib( 6): 8
fib( 7): 13
fib( 8): 21
fib( 9): 34
fib(10): 55
fib(11): 89
fib(12): 144
fib(13): 233
fib(14): 377
fib(15): 610
fib(16): 987
fib(17): 1597
fib(18): 2584
fib(19): 4181
fib(20): 6765
fib(21): 10946
fib(22): 17711
fib(23): 28657
fib(24): 46368
fib(25): 75025
fib(26): 121393
fib(27): 196418
fib(28): 317811
fib(29): 514229
fib(30): 832040
fib(31): 1346269
fib(32): 2178309
fib(33): 3524578
fib(34): 5702887
fib(35): 9227465
fib(36): 14930352
fib(37): 24157817
fib(38): 39088169
fib(39): 63245986
fib(40): 102334155
fib(41): 165580141
fib(42): 267914296
fib(43): 433494437
fib(44): 701408733
fib(45): 1134903170
fib(46): 1836311903
fib(47): 2971215073
fib(48): 4807526976
fib(49): 7778742049
fib(50): 12586269025
fib(51): 20365011074
fib(52): 32951280099
fib(53): 53316291173
fib(54): 86267571272
fib(55): 139583862445
fib(56): 225851433717
fib(57): 365435296162
fib(58): 591286729879
fib(59): 956722026041
fib(60): 1548008755920
fib(61): 2504730781961
fib(62): 4052739537881
fib(63): 6557470319842
fib(64): 10610209857723
fib(65): 17167680177565
fib(66): 27777890035288
fib(67): 44945570212853
fib(68): 72723460248141
fib(69): 117669030460994
fib(70): 190392490709135
fib(71): 308061521170129
fib(72): 498454011879264
fib(73): 806515533049393
fib(74): 1304969544928657
fib(75): 2111485077978050
fib(76): 3416454622906707
fib(77): 5527939700884757
fib(78): 8944394323791464
fib(79): 14472334024676221
fib(80): 23416728348467685
fib(81): 37889062373143906
fib(82): 61305790721611591
fib(83): 99194853094755497
fib(84): 160500643816367088
fib(85): 259695496911122585
fib(86): 420196140727489673
fib(87): 679891637638612258
fib(88): 1100087778366101931
fib(89): 1779979416004714189
fib(90): 2880067194370816120
fib(91): 4660046610375530309
fib(92): 7540113804746346429
fib(93): 12200160415121876738
fib(94): 19740274219868223167
fib(95): 31940434634990099905
fib(96): 51680708854858323072
fib(97): 83621143489848422977
fib(98): 135301852344706746049
fib(99): 218922995834555169026
fib(100): 354224848179261915075
fib(12345): 400805695072240470970514993214065752192289440772063392234116121035966330621821050108284603033716632771086638046166577665205834362327397885009536790892524821512145173749742393351263429067658996935575930135482780507243981402150702461932551227590433713277255705297537428017957026536279252053237729028633507123483103210846617774763936154673522664591736081039709294423865668046925492747583953758325850613548914282578320544573036249175099094644435323970587790740267131607004023987409385716162460955707793257532112771932704816713519196128834470721836094265012918046427449156654067195071358955104097973710150920536847877434256779886729555691213282504703193401739340461924048504866698176130757935914248753973087073009601101912877383634628929467608983980664185363370286731771712542583041365328648124549323878806758395652340861186334027392307091079257180835672989798524084534677252369585918458720952520972332496025465803523315515681084895362126005441170936820059518262349022456888758938672920855739736423917065122816343192172271301981007636070751378441363091187289522144227851382197807194256392294919912037019476582418451273767976783751999133072126657949249799858935787018952232743400610036315564885371356712960608966755186612620425868892621106627825137425386831657368826398245606147944273998498356443362170133234924531673939303668042878258282104212769625245680321344034442698232414181912301904509531018692483863038992377680591406376081935756597411807864832452421993121459549055042253305545594009110753730302061881025182053074077930494574304284381890534053065639084253641881363463311184024281835265103884539012874542416238100890688593076189105555658375552988619203325356676814545718066196038345684671830102920209857682912971565838896011294918349088792184108318689299230788355618638040186790724351073650210514429114905535411044888774713860041341593318365792673354888566799196442017231870631867558530906286613228902689695061557951752309687806567573290910909535395758148994377158637050112347651517847188123790794231572729345617619677555583207012253101701328971768827861922408064379891201972881554890367344239218306050355964382953279316318309272212482218232309006973312977359562553184608144571713073802285675503209229581312057259729362382786183100343961484090866057560474044189870633912200595478051573769889968342203512550302655117491740823696686983281784153050366346823513213598551985596176977626982962058849363351794302206703907577970065793839511591930741441079234179943480206539767561244271325923343752071038968002157889912694947204003637791271084190929058369801531787887444598295425899927970
Подсказки:
test_seq() не очень умен, он не использовал кеш между двумя входными test_seq(). fib_gmp() будет достаточно, если вы добавите gmp_printf() в fib_gmp_next() и предоставите я для fib_gmp_next() на каждом шаге. вот короткий код на Python, хорошо работает до 7 цифр. Просто требуется массив из 3 элементов
def fibo(n):
i=3
l=[0,1,1]
if n>2:
while i<=n:
l[i%3]= l[(i-1) % 3] + l[(i-2) % 3]
i+=1
return l[n%3]
Более элегантное решение в python
def fib(n):
if n == 0:
return 0
a, b = 0, 1
for i in range(2, n+1):
a, b = b, a+b
return b
Я написал небольшой код для вычисления Фибоначчи для большого числа, который быстрее, чем метод речевой речи.
Я использую метод запоминания, чтобы получить последнее число Фибоначчи вместо того, чтобы перепрограммировать его.
public class FabSeries {
private static Map<BigInteger, BigInteger> memo = new TreeMap<>();
public static BigInteger fabMemorizingTech(BigInteger n) {
BigInteger ret;
if (memo.containsKey(n))
return memo.get(n);
else {
if (n.compareTo(BigInteger.valueOf(2)) <= 0)
ret = BigInteger.valueOf(1);
else
ret = fabMemorizingTech(n.subtract(BigInteger.valueOf(1))).add(
fabMemorizingTech(n.subtract(BigInteger.valueOf(2))));
memo.put(n, ret);
return ret;
}
}
public static BigInteger fabWithoutMemorizingTech(BigInteger n) {
BigInteger ret;
if (n.compareTo(BigInteger.valueOf(2)) <= 0)
ret = BigInteger.valueOf(1);
else
ret = fabWithoutMemorizingTech(n.subtract(BigInteger.valueOf(1))).add(
fabWithoutMemorizingTech(n.subtract(BigInteger.valueOf(2))));
return ret;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter Number");
BigInteger num = scanner.nextBigInteger();
// Try with memorizing technique
Long preTime = new Date().getTime();
System.out.println("Stats with memorizing technique ");
System.out.println("Fibonacci Value : " + fabMemorizingTech(num) + " ");
System.out.println("Time Taken : " + (new Date().getTime() - preTime));
System.out.println("Memory Map: " + memo);
// Try without memorizing technique.. This is not responsive for large
// value .. can 50 or so..
preTime = new Date().getTime();
System.out.println("Stats with memorizing technique ");
System.out.println("Fibonacci Value : " + fabWithoutMemorizingTech(num) + " ");
System.out.println("Time Taken : " + (new Date().getTime() - preTime));
}
}
Введите номер
40
Статистика с техникой запоминания
Значение Фибоначчи: 102334155
Время: 5
Карта памяти: {1 = 1, 2 = 1, 3 = 2, 4 = 3, 5 = 5, 6 = 8, 7 = 13, 8 = 21, 9 = 34, 10 = 55, 11 = 89, 12 = 144, 13 = 233, 14 = 377, 15 = 610, 16 = 987, 17 = 1597, 18 = 2584, 19 = 4181, 20 = 6765, 21 = 10946, 22 = 17711, 23 = 28657, 24 = 46368, 25 = 75025, 26 = 121393, 27 = 196418, 28 = 317811, 29 = 514229, 30 = 832040, 31 = 1346269, 32 = 2178309, 33 = 3524578, 34 = 5702887, 35 = 9227465, 36 = 14930352, 37 = 24157817, 38 = 39088169, 39 = 63245986, 40 = 102334155}
Статистика без запоминания техники
Значение Фибоначчи: 102334155
Время: 11558
Если вы используете С#, взгляните на Lync и BigInteger. Я пробовал это с 1000000 (фактически 1000001, поскольку я пропускаю первый 1000000) и был ниже 2 минут (00: 01:19.5765).
public static IEnumerable<BigInteger> Fibonacci()
{
BigInteger i = 0;
BigInteger j = 1;
while (true)
{
BigInteger fib = i + j;
i = j;
j = fib;
yield return fib;
}
}
public static string BiggerFib()
{
BigInteger fib = Fibonacci().Skip(1000000).First();
return fib.ToString();
}
#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
const long long int MAX = 10000000;
// Create an array for memoization
long long int f[MAX] = {0};
// Returns n'th fuibonacci number using table f[]
long long int fib(int n)
{
// Base cases
if (n == 0)
return 0;
if (n == 1 || n == 2)
return (f[n] = 1);
if (f[n])
return f[n];
long long int k = (n & 1)? (n+1)/2 : n/2;
f[n] = (n & 1)? (fib(k)*fib(k) + fib(k-1)*fib(k-1)) %MOD
: ((2*fib(k-1) + fib(k))*fib(k))%MOD;
return f[n];
}
int main()
{
long long int n = 1000000;
printf("%lld ", fib(n));
return 0;
}
Сложность времени: O (Log n), когда мы делим проблему на половину в каждом рекурсивном вызове.
Вычисление чисел фибоначчи (с использованием Haskell):
Версия 1: прямой перевод определения в код (очень медленная версия):
fib :: Integer -> Integer
fib 0 = 1
fib 1 = 1
fib n =
fib (n - 1) + fib (n - 2)
Версия 2. Используя работу, которую мы проделали для вычисления F_ {n - 1} и F_ {n - 2} (быстрая версия):
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
Вы можете получить n-й фибоначчи, просто сделав fibs !! n, где n - индекс.
Версия 3: использование метода матричной мультипликации. (более быстрая версия):
-- declaring a matrix
data Matrix = Matrix
( (Integer, Integer)
, (Integer, Integer)
)
deriving (Show, Eq)
-- creating it an instance of Num
-- so that if we implement (*) we get (^) for free
instance Num Matrix where
(*) = mMult
-- don't need these
(+) = undefined
negate = undefined
fromInteger = undefined
abs = undefined
signum = undefined
-- 2-d matrix multiplication
mMult :: Matrix -> Matrix -> Matrix
mMult (Matrix ((a11, a12), (a21, a22))) (Matrix ((b11, b12), (b21, b22))) =
Matrix
( (a11 * b11 + a12 * b21, a11 * b12 + a12 * b22)
, (a21 * b11 + a22 * b21, a21 * b12 + a22 * b22)
)
-- base matrix for generating fibonacci
fibBase :: Matrix
fibBase =
Matrix ((1,1), (1,0))
-- get the large fibonacci numbers
fastFib :: Int -> Integer
fastFib n =
let
getNth (Matrix ((_, a12), _)) = a12
in
getNth (fibBase ^ n)
Я сделал программу. Это не займет много времени, чтобы рассчитать значения, но максимальный срок, который может быть отображен, - 1477-й (из-за максимального диапазона для двойного). Результаты появляются почти мгновенно. Серия начинается с 0. Если есть какие-либо улучшения, пожалуйста, не стесняйтесь редактировать их.
#include<iostream>
using namespace std;
void fibseries(long int n)
{
long double x=0;
double y=1;
for (long int i=1;i<=n;i++)
{
if(i%2==1)
{
if(i==n)
{
cout<<x<<" ";
}
x=x+y;
}
else
{
if(i==n)
{
cout<<x<<" ";
}
y=x+y;
}
}
}
main()
{
long int n=0;
cout<<"The number of terms ";
cin>>n;
fibseries(n);
return 0;
}
Простейшая реализация Pythonic может быть задана следующим образом
def Fib(n):
if (n < 0) :
return -1
elif (n == 0 ):
return 0
else:
a = 1
b = 1
for i in range(2,n+1):
a,b = b, a+b
return a
Эта реализация JavaScript обрабатывает nthFibonacci (1200) без проблем:
var nthFibonacci = function(n) {
var arr = [0, 1];
for (; n > 1; n--) {
arr.push(arr.shift() + arr[0])
}
return arr.pop();
};
console.log(nthFibonacci(1200)); // 2.7269884455406272e+250
Имея некоторые знания в области дискретной математики, вы можете найти любое число Фибоначчи за постоянное время O (1). Существует нечто, называемое линейно-однородным рекуррентным отношением.
Последовательность Фибоначчи является известным примером.
Чтобы найти n-е число Фибоначчи, нам нужно найти
Мы знаем это
где
Тогда характеристическое уравнение
После нахождения корней характеристического уравнения и подстановки в первое уравнение
Наконец, нам нужно найти значение как альфа 1 и альфа 2
Теперь вы можете использовать это уравнение, чтобы найти любое число Фибоначчи в O (1).